電気二重層コンデンサの静電容量によるバックアップ時間の考え方

こんにちは、ENGかぴです。

電子回路設計において電源が切れてもSRAMやRTCなどのデータを保持するために電気二重層コンデンサを使ってバックアップすることがあります。電気二重層コンデンサの容量と電圧の関係からバックアップ時間の計算の仕方についてまとめました。

電気二重層コンデンサ以外のコンデンサにおいても同様に考えることができます。

コンデンサの容量と電圧の関係
コンデンサの漏れ電流の考え方
- 漏れ電流（自己放電）に注意
- 漏れ電流を計算する
バックアップ時間を考えかた
関連リンク

コンデンサの容量と電圧の関係

コンデンサは電荷を蓄えることができるためバックアップに使われたり清流後の波形のリップルの平滑化などに使われたり用途は様々です。

今回はバックアップによく使用される電気二重層コンデンサによるバックアップ時間を考えます。

コンデンサの電極にたまる電荷Qの量を電気量といい、その単位はC「クーロン」です。電荷量と電流との関係は時間の積分で表されます。$$Q = \int{I(t)dt}・・(1)$$

これは、電気量は瞬間的に流れる電流の時間の和であることを意味します。そして1秒間に１Aの電流が流れた時運ばれる電気量が１Cと定義しています。

式(1)においてI(t)が一定もしくは平滑化された電流としたとき以下のように定義することができます。$$Q = I\times t （は時間で単位は秒）・・(2)$$

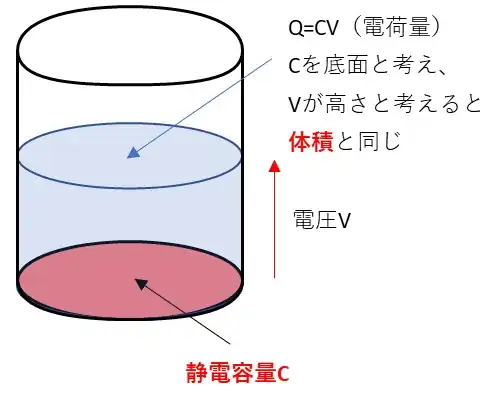
１Vの電池をつないだ時１Cの電荷を蓄えることのできるコンデンサは1F「ファラド」の静電容量Cを持つと言い、$$Q=C\times V・・(3)$$の関係が成り立ちます。

コンデンサは、2つの端子に直流電圧Vを印加すると電気を蓄えることができます。そのエネルギーはW[ J ]　は$$W = \frac{1}{2}CV^2・・(4)$$となります。電圧が高いほど二乗分だけエネルギーが増すということになります。単位[J]ジュールは[W・ｓ]ワット秒でもあるため電源から流入する電力からバックアップ時間を求めたり、必要なコンデンサ容量を求めたりすることができます。

(1)から(4)の式の組み合わせでバックアップ時間とコンデンサ容量を用途に応じて計算することができます。

コンデンサの漏れ電流の考え方

コンデンサは電荷を蓄えることできますが、同時に電気が抜けていきます。これを漏れ電流といいます。漏れ電流は電源のワット数（エネルギーが大きい）ければそこまで問題になりませんが、エナジーハーベストなどの微小な電圧であれば問題になります。

漏れ電流（自己放電）に注意

コンデンサは充電して端子を開放したまま放置しても漏れ電流（自己放電）によって電荷が失われていきます。

漏れ電流が大きいほど蓄えた電荷が抜けていく時間が早くなってしまいます。

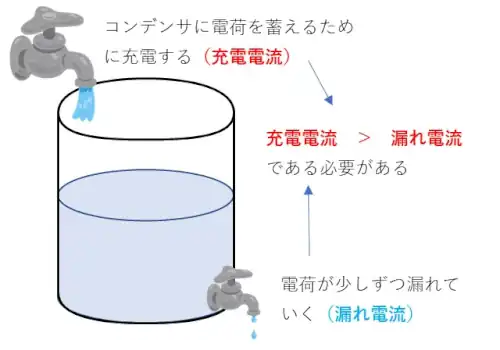
身近な例で言うと穴の開いた容器に水を入れているのと同じことです。穴が大きいほど水がすぐに抜けるのと同じです。

コンデンサに充電される電流と漏れ電流の関係
充電電流　＞　漏れ電流

であればコンデンサに充電することができます。トーキン製の電気二重層コンデンサの仕様を見て漏れ電流を見てみます。FGタイプは500uA以下の負荷に使用するバックアップ用のコンデンサです。

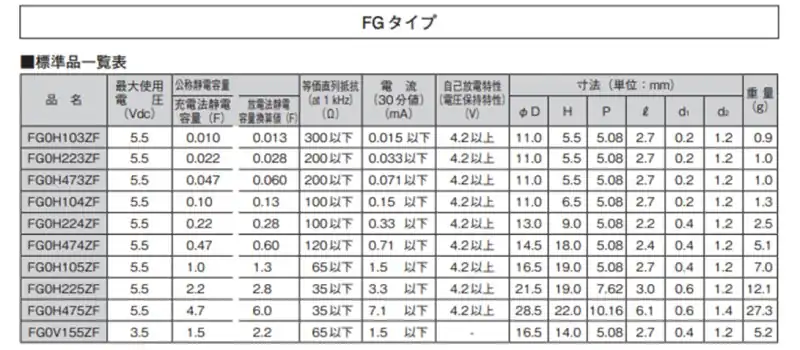
自己放電特性（電圧保持特性）が漏れ電流の仕様になります。厳密に言うと電気二重層コンデンサにおいては長時間電流特性というのがあり数十時間~数百時間通電して電流がほぼ一定になった電流値を漏れ電流とすることもありますが、24時間で見たときは自己放電特性で漏れ電流を考えても問題ありません。

漏れ電流を計算する

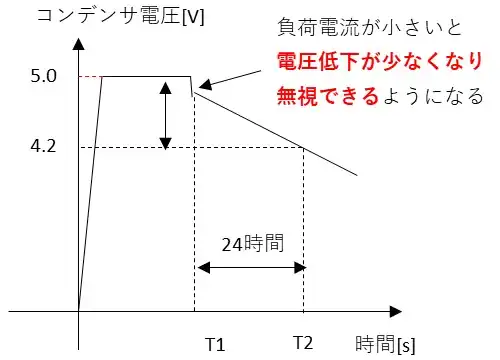
トーキンのデータシートで自己放電特性の測定条件を見ると充電条件が印加電圧が5.0Vdc、充電保護抵抗0Ω、充電時間が24時間でその後周囲温度25℃以下相対湿度70％RH以下で放置となっています。

放置した後の保持電圧が4.2V以上となってなっているため24時間で0.8V低下することが最悪な条件ということになります。

端子を開放で放置していることから空気放電となることから漏れ電流がかなり微小であるとみなせるので等価抵抗による電圧低下は無視して考えます。

漏れ電流は周囲温度25℃などの条件により一定であると考えることができます。漏れ電流が一定なので(2)式を使って考えることができます。$$Q = I\times(24\times60 \times60 )・・24時間分の秒数$$

また(3)式によって放置した時間に失われた電荷量を求めることができます。$$Q=C\times 0.8$$(2)=(3)でありCを1Fの電気二重層コンデンサを選択したとすると、$$I = \frac{1\times0.8}{(24\times60\times60)}= 9.26uA$$

よって最悪な条件で9.26uAが漏れていることになります。

バックアップ時間を考えかた

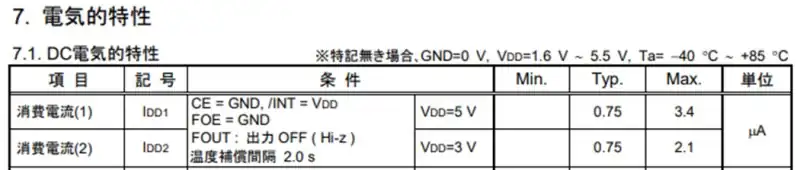
電気二重層コンデンサ１Fを使ってRTCのバックアップ時間について考えてみます。RTCはエプソン製のRX-4803SA(電圧範囲1.6V、バックアップ電流0.75uA)を例にして説明します。

電圧範囲は余裕を見て2Vとし、バックアップ電流も最大値を採用してを入れて3.4uAとして計算します。RX-4803SAのFOUT出力はOFFを前提にしています。

電気二重層コンデンサの漏れ電流は9.26uAでRTCは最大で3.4uAが必要になるので合計12.66uAが消費されることになります。(2)式において$$Q = 12.66uA\times s$$となり、(3)式において電圧が5Vから2Vまで低下するまでとするとVは3Vとなるので、$$Q=1\times 3$$(2)=(3)から$$s = \frac{1\times3}{12.66\times10^{-6}}= 236967秒 = 3950分 = 66時間$$

66時間程度のバックアップが可能になります。漏れ電流の計算は最悪の場合を想定していることやRTCにおいても最悪の条件としているので66時間以上のバックアップが可能であると言えますが、電気二重層コンデンサは温度特性によって漏れ電流や容量が変化するがあるので目安程度にとどめておいたほうが良いと思います。

静電容量を固定してバックアップ時間を計算しましたが、式(2)と式(3)を応用することでバックアップしたい時間から必要な容量を計算することができます。