【電気電子部門】技術士第一次試験のコンデンサ問題の解説

こんにちは、ENGかぴです。

技術士第一次試験の電気電子部門の試験において最近コンデンサ関係の問題が出題されています。一つのコンデンサに電荷をチャージしておき2つ目のコンデンサを並列に接続したときの静電エネルギーや全体の電圧などが分かっていれば難しくありません。コンデンサの接続方法による容量の考え方をまとめています。

技術士第一次試験の勉強におすすめする参考書や電気電子部門のポイント解説についてまとめています。これらのシリーズで2か月間勉強することで十分合格できます。

【電気電子部門】技術士第一次試験の勉強におすすめの参考書3選

コンデンサ問題のポイント解説
コンデンサの静電容量
関連するリンク

コンデンサ問題のポイント解説

コンデンサの容量とエネルギーに関する問題が増えていると思います。平成29年度以降で出題が多くなっていると感じます。解き方が分かっていれば簡単に解けるためポイント解説したいと思います。公開されている過去問を引用して説明していきます。

R2年度の問題（電荷の移動による比率）

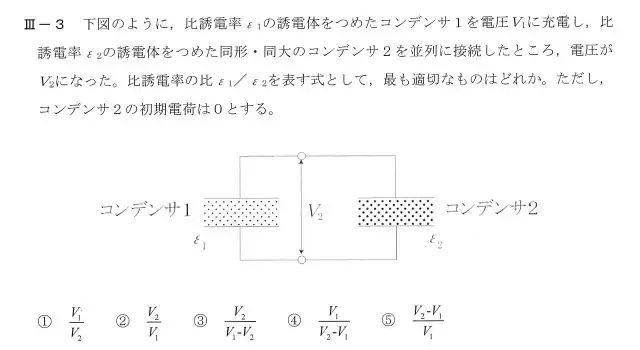
この問題のポイントは誘電体挿入前の電荷が挿入後のコンデンサにおいても同じであること、静電容量が変化することにより電圧が変化することです。並行板コンデンサの静電容量から求めます。

コンデンサ1の静電容量をC₁、コンデンサ2の静電容量をC₂とします。2つのコンデンサは同形・同大であるから並行板コンデンサの面積をS、平板間の距離をdとすると以下のようになります。$$C_1=\frac{ε_1S}{d}、C_2=\frac{ε_2S}{d}$$となります。V₁に充電したC₁にC₂を接続するため接続の前後での電荷の総量が変わらないことから以下のようになります。$$C_1V_1 = (C_1+C_2)V_2$$$$\frac{ε_1S}{d}V_1=(\frac{ε_1S}{d}+\frac{ε_2S}{d})V_2$$$$ε_1V_1=(ε_1+ε_2)V_2$$$$\frac{ε_1}{ε_2}=\frac{V_2}{V_1-V_2}$$となります。従って、③が正解になります。

R1年度（再試験）の問題（複合コンデンサ）

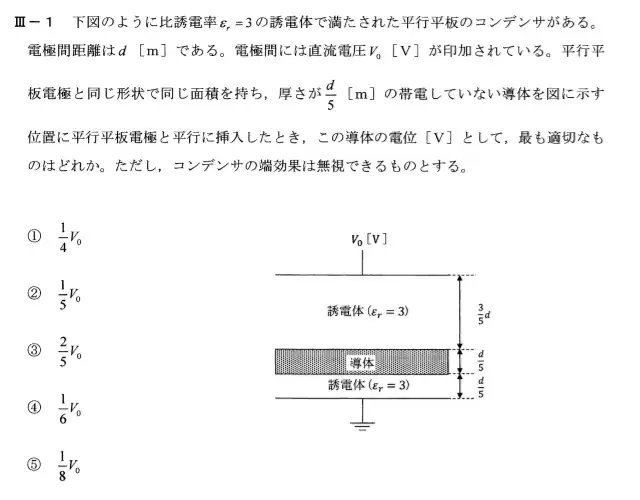
この問題のポイントは導体を挿入していることです。導体とは簡単に言うと金属です。金属は電気を通すので抵抗がなく電線で繋いでいるのと同じ扱いができます。

問題を導体の部分を踏まえると以下のように考えることができます。

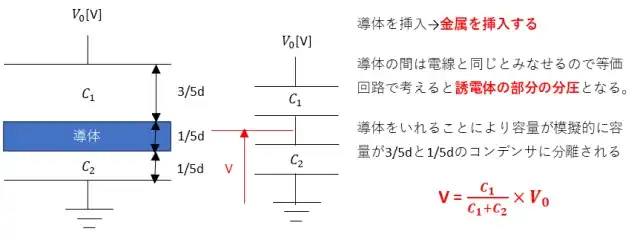
誘電体が含まれているコンデンサが２つ直列につないだ回路となります。導体部分の電圧はC₂（導体下の部分）の電圧がそのまま導体部分の電圧になります。C₁とC₂のコンデンサ容量を計算してコンデンサの比で電圧を求めると答えになります。

平行平板コンデンサの容量は、真空の誘電率をε₀誘電率をε_r平行平板の極板の面積をS厚さがdとしたときコンデンサの静電容量は$$C_0=\frac{ε_0}{ε_rS}{d}$$となります。詳細は平行板コンデンサの考え方を参考にしてください。導体を挿入する前のコンデンサの静電容量はC₀とするとC₁とC₂は$$C_1=\frac{ε_0ε_rS}{\frac{3}{5}d}=\frac{5}{3}C_0$$$$C_2=\frac{ε_0ε_rS}{\frac{1}{5}d}=5C_0$$導体の電圧VはC₂の電圧と同じなのでコンデンサの静電容量の比から電圧を求めると、$$V = \frac{C_1}{C_1+C_2}V_0 = \frac{\frac{5}{3}C_0}{\frac{5}{3}C_0+ 5C_0}V_0= \frac{1}{4}V_0$$したがって①が正解となります。

R1年度の問題（コンデンサのエネルギー）

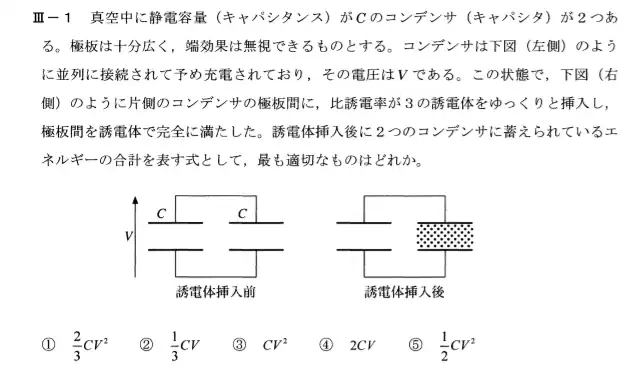
この問題のポイントは誘電体挿入前の電荷が挿入後のコンデンサにおいても同じであること、静電容量が変化することにより電圧が変化することです。容量の変化と電圧の変化から誘電体挿入後のエネルギーを求める必要があります。

誘電体挿入前の静電容量はコンデンサが２つ並列に接続されているのでC+C＝2Cになります。Q=CVの関係から誘電体挿入前の電荷はQ₀=2CVになります。

誘電体を挿入すると挿入されたコンデンサの静電容量が変化します。平行板コンデンサの考え方の（１）式により比誘電率が3の誘電体を挿入すると静電容量は$$C’=\frac{3×ε_0S}{d}= 3C$$

となりCとC’が並列に接続されているので静電容量はC”＝C+3C=4Cになります。この時の電圧V’は誘電体の挿入前後の電荷の量が同じであることから$Q_0 = 2CV = 4CV’$となるので$V’=\frac{1}{2}V$となります。コンデンサに蓄えられるエネルギーWは、$$W=\frac{1}{2}CV^2= \frac{1}{2}×4C×(\frac{1}{2}V)^2=\frac{1}{2}CV^2$$したがって⑤が正解となります。

コンデンサの静電容量

コンデンサの静電容量について平行板コンデンサのから複合コンデンサについて説明します。複合コンデンサは平行板の間の誘電体（絶縁物）が多種類のものからできている平行板コンデンサのことです。

平行板コンデンサの静電容量

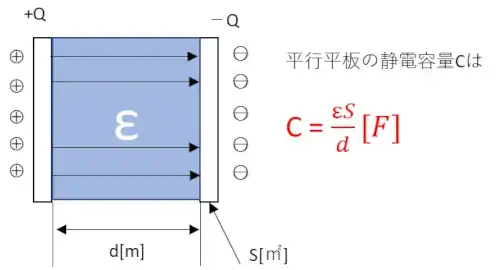
面積がS[㎡]の2枚の導体をd[m]の間隔で平行におきその間に誘電率εの媒質で満たしたときの平行板間の静電容量は+Qと-Qの電荷を与えたものとして、導体板は平行なので電気力線は+から－の向きに分布します。

一様に分布するので平行平板間のどの点も電界の強さも一定になります。電気力線は電荷Qから出るもので全電気力線の数はQ/ε[本](真空の誘電率をε₀、比誘電率をε_rとしたときの誘電率εはε= ε₀×ε_r)になります。電界の強さは電気力線の密度であるので$E= \frac{Q}{εS} [V/m]$となります。

この平行板間は平等電界だから導体間の電位差Vは$V= E×d =\frac{Qd}{εS} [V]$となります。Q=CVから静電容量Cは

$$C = \frac{Q}{V}= \frac{εS}{d}[F]・・(1)$$

となります。

複合コンデンサ（直列形）の静電容量

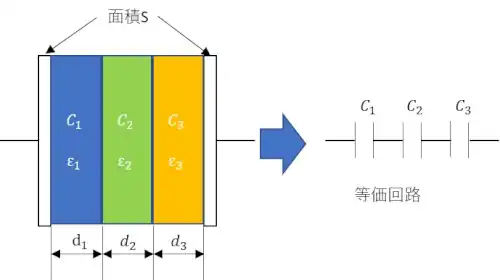
面積S[㎡]の平行板の中に誘電率がε₁、ε₂、ε₃がありそれぞれの比誘電率をε_ｒ1、ε_ｒ2、ε_ｒ3としたときのそれぞれの静電容量C₁、C₂、C₃をすると等価回路はC₁、C₂、C₃を直列につないだ回路になります。

この時のそれぞれの静電容量は（１）式より以下の通りです。

$$C_1=\frac{ε_0ε_{r1}S}{d_1}、C_2=\frac{ε_0ε_{r2}S}{d_2}、 C_3=\frac{ε_0ε_{r3}S}{d_3}$$となります。したがって、直列合成の静電容量Cは

$$C=\frac{1}{\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}} = \frac{ε_0S}{\frac{d_1}{ε_{r1}}+\frac{d_2}{ε_{r2}}+\frac{d_3}{ε_{r3}}}・・(2)$$

となります。誘電体が何種類からなっていても同様に求めることができます。

複合コンデンサ（並列形）の静電容量

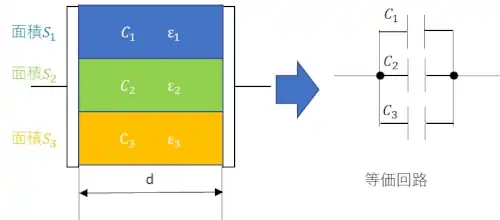
電極間の距離がd[m]で極板の面積S₁[㎡]の誘電率がε₁、面積S₂[㎡]の誘電率がε₂、面積S₃[㎡]の誘電率がε₃がありそれぞれの比誘電率をε_ｒ1、ε_ｒ2、ε_ｒ3としたときのそれぞれの静電容量C₁、C₂、C₃をすると等価回路はC₁、C₂、C₃を並列につないだ回路になります。

この時のそれぞれの静電容量は（１）式より以下の通りです。$$C_1=\frac{ε_0ε_{r1}S_1}{d}、C_2=\frac{ε_0ε_{r2}S_2}{d}、 C_3=\frac{ε_0ε_{r3}S_3}{d}$$となります。したがって、並列合成の静電容量Cは

$$C=C_1+C_2+C_3=\frac{ε_0}{d}(ε_{r1}S_1+ε_{r2}S_2+ε_{r3}S_3)・・(3)$$

と表すことができます。誘電体が何種類からなっていても同様に求めることができます。