【電気電子部門】技術士第一次試験の相互インダクタンス問題の解説

こんにちは、ENGかぴです。

技術士第一次試験の電気電子部門の試験において最近相互インダクタンスの問題が出題されています。自己インダクタンスと相互インダクタンスの関係が分かっていれば簡単に解ける問題です。インダクタンスの定義などについてもまとめています。

技術士第一次試験の勉強におすすめする参考書や電気電子部門のポイント解説についてまとめています。これらのシリーズで2か月間勉強することで十分合格できます。

相互インダクタンスの問題のポイント解説
- H29年の相互インダクタンスの問題
- R1（再試験）の相互インダクタンスの問題
インダクタンス
関連するリンク

相互インダクタンスの問題のポイント解説

最近の出題傾向として相互インダクタンスを問う問題が出題されています。これは相互インダクタンスの意味が分かっていれば簡単に答えることができます。解き方が分かっていれば簡単に解けるためポイント解説したいと思います。公開されている過去問を引用して説明していきます。

H29年の相互インダクタンスの問題

この問題を図示すると下の項目で説明している相互インダクタンスの図になります。この図においてN₁側がコイルAとしN₂側がコイルBとして考えてきます。コイルA側に電流流したときの磁束をΦ₁としたとき一次側の自己インダクタンスをL₁[H]、一次側と二次側コイル間の相互インダクタンスをM[H]とするとL₁およびMは、$$L_1=N_1×Φ_1$$ $$M= N_2×Φ_1=\frac{N_2}{N_1}L_1[H]$$となります。$$M = \frac{400}{5000}500 = 40[mH]$$結合係数kを考慮する必要があるので$$M’ = kM = 1×40 = 40[mH]$$となるので②が正解となります。

R1（再試験）の相互インダクタンスの問題

この問題を図示すると下の項目で説明している相互インダクタンスの図になります。この図においてN₁側がコイルAとしN₂側がコイルBとして考えてきます。コイルA側に電流流したときの磁束をΦ₁としたとき一次側の自己インダクタンスをL₁[H]、一次側と二次側コイル間の相互インダクタンスをM[H]とするとL₁およびMは、$$L_1=N_1×Φ_1$$ $$M= N_2×Φ_1=\frac{N_2}{N_1}L_1[H]$$となります。$$M = \frac{500}{4000}400 = 50[mH]$$結合係数kを考慮する必要があるので$$M’ = kM = 0.96×50 = 48[mH]$$となるので③が正解となります。

インダクタンス

相互インダクタンスを求めるにあたってインダクタンスとは何かについて自己インダクタンスと相互インダクタンスの関係について説明します。

自己インダクタンス

コイルの電流を変化させるとレンツの法則より誘導起電力が発生します。

この誘導起電力の向きはコイルに加えた電圧とは逆向きになるので逆起電力といいます。

コイルの巻き数をNとすると逆起電力は$$E = -N\frac{ΔΦ}{Δt}$$となります。磁束の変化ΔΦは電流の変化ΔIに比例する（透磁率が一定とする）から比例定数をLとしたとき$$E=-N\frac{ΔΦ}{Δt}= – L\frac{ΔI}{Δt}・・(1)$$

この比例定数を自己インダクタンスとしています。コイルに1秒間1[A]の電流変化を与えたときコイルに1[V]を変化があるとすると自己インダクタンスは1[H]となります。

式(1)よりNΦ=LIとなるので$$L = \frac{NΦ}{I}・・(2)$$となります。

相互インダクタンス

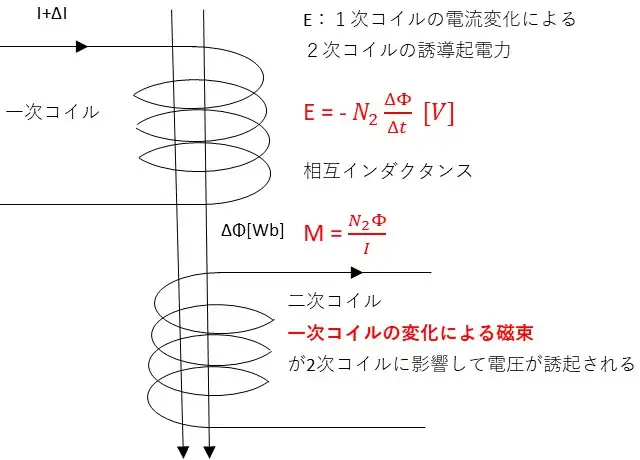
二次コイルの巻数をN₂として一次コイルの電流がΔI[A]だけ変化した時二次コイルと鎖交する磁束がΔΦ[Wb]だけ変化したものとします。

２次コイルに誘起される電圧はレンツの法則より$$E = -N_2\frac{ΔΦ}{Δt}$$磁束の変化ΔΦは電流の変化ΔIに比例する（透磁率が一定とする）から比例定数をMとしたとき$$E=-N_2\frac{ΔΦ}{Δt}= – M\frac{ΔI}{Δt}・・(3)$$

この比例定数を相互インダクタンスとしています。一次コイルに1秒間1[A]の電流変化を与えたとき２次コイルに1[V]を変化があるとすると相互インダクタンスは1[H]となります。

式(1)よりN₂Φ=MIとなるので$$M = \frac{N_2Φ}{I}・・(4)$$となります。

自己インダクタンスと相互インダクタンス

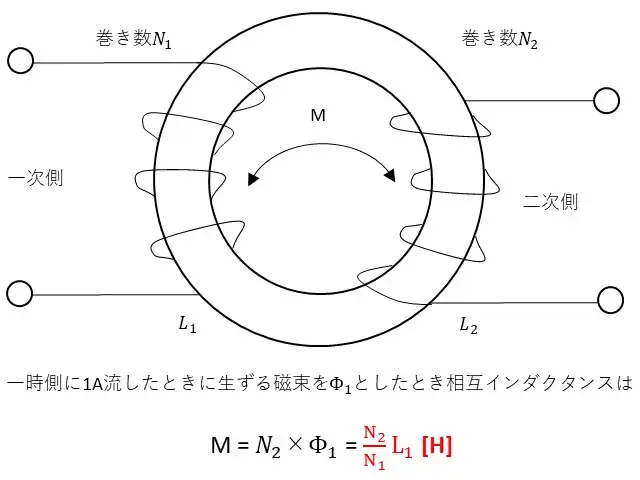
自己インダクタンスと相互インダクタンスの関係について説明します。共通の環状の鉄心を磁路にもつ２つのコイルがあって一時側の巻き数をN₁二次側の巻き数をN₂とし、両コイル間には漏れ磁束がないものとします。

式(2)より一次側に１[A]を流したときに生ずる磁束をφ₁[Wb]一次側の自己インダクタンスをL₁[H]、一次側と二次側コイル間の相互インダクタンスをM[H]とするとL₁およびMは、$$L_1=N_1×Φ_1$$

$$M= N_2×Φ_1=\frac{N_2}{N_1}L_1[H]・・(5)$$

となります。

同じように二次側に1[A]を流したときに生じる磁束をΦ₂[Wb]二次側の自己インダクタンスをL₂[H]とすると$$L_2=N_2×Φ_2$$ $$M= N_1×Φ_2=\frac{N_1}{N_2}L_2[H]・・(6)$$となります。

(5)(6)から$$M^2=L_1L_2$$ $$M = ±\sqrt{L_1L_2}・・(7)$$と表すことができます。実際には漏れ電流があるので、一次側のつくる磁束が全部が二次側のコイルに鎖交せず(7)の値より少し小さくなるため$M<\sqrt{L_1L_2} $となります。この時、$ M=±k\sqrt{L_1L_2}$としたとき、$$k=\frac{M}{\sqrt{L_1L_2}}$$とおいたときこのｋを結合係数といいます。結合係数は電磁結合の程度を表す値としており、コイルの位置、形状、寸法によって0から1までの範囲で表されます。