【電気電子部門】技術士第一次試験の電荷に関する問題の解説

こんにちは、ENGかぴです。

技術士第一次試験の電気電子部門の試験において電荷の問題が出題されています。点電荷に関するクーロンの法則や電界の関係が分かっていれば簡単に解ける問題です。電荷に関する問題の解き方や電解と電位の関係性などをまとめています。

技術士第一次試験の勉強におすすめする参考書や電気電子部門のポイント解説についてまとめています。これらのシリーズで2か月間勉強することで十分合格できます。

【電気電子部門】技術士第一次試験の勉強におすすめの参考書3選

電荷に関する問題のポイント解説
点電荷の考え方
1. 電界とクーロン力の関係
2. 電界と電位
関連するリンク

電荷に関する問題のポイント解説

点電荷の電界に関する問題が増えていると思います。平成29年度以降で出題が多くなっていると感じます。解き方が分かっていれば簡単に解けるためポイント解説したいと思います。公開されている過去問を引用して説明していきます。

R2年度の問題（電荷が作る電位）

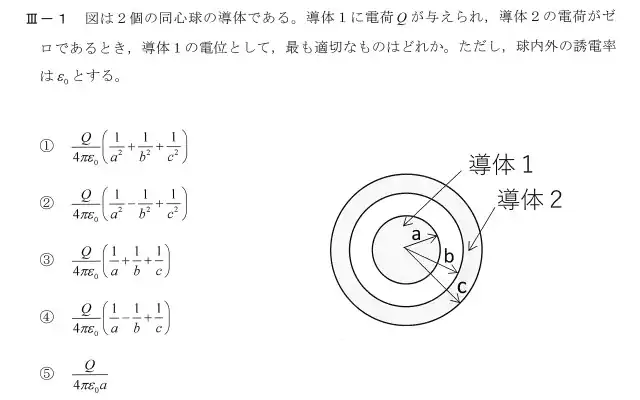
この問題のポイントは導体2の電荷がゼロであるときの導体2の状態が分かるかです。導体1から+Qの電荷からの電界による影響から導体2の内側の表面に－の電荷が発生します。導体2の電荷がゼロになるように+の電荷が外側の表面に集まり－と+の電荷の移動が終わると導体2の内部の電界が0になります。そのため導体2内では電位は同電位になります。

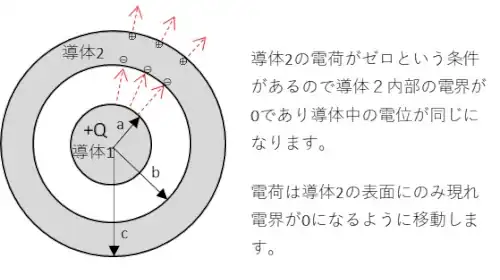
問題の題意から導体2の電荷がゼロになるように導体2の表面に電荷が移動したとすると赤点線のように電気力線が進むためーの電荷が内部の表面、+の電荷が外側の表面に分布します。導体1による電界を求めて電位を算出します。

導体1のQからr[m]離れた点の電界Eはガウスの定理から以下の通りになります。$$4πr^2・E = \frac{Q}{ε_0}$$$$E=\frac{1}{4πε_0}・\frac{Q}{r^2}$$となります。電位Vは電界を無限遠から積分したもの(電界と電位参照)であるから$$V = -\int_∞^rE・dr=-\int_b^a\frac{Q}{4πε_0r^2}dr-\int_∞^c\frac{Q}{4πε_0r^2}dr$$$$V=\frac{Q}{4πε_0}[\frac{1}{r}]^a_b+\frac{Q}{4πε_0}[\frac{1}{r}]^c_∞ = \frac{Q}{4πε_0}(\frac{1}{a}-\frac{1}{b}+\frac{1}{c})$$となります。従って、正解は④になります。

R1年度の問題（点電荷の電位と電界）

この問題のポイントは重心位置Gの電位が0Vであること電界のベクトルの考え方による大きさと向きです。電位はスカラ（大きさ）で考えてよいのに対して電界はベクトルで考える必要があります。

G点での電位が0Vという条件からG点での電位を求めます。この時のD点の電荷をQxとします。G点の電位はA、B、C、D点の電荷による電位を加えればよく以下のようになります。

$$Aによる電位= \frac{Q}{4πε_0a}、Bによる電位=\frac{-Q}{4πε_0a}$$$$Cによる電位=\frac{3Q}{4πε_0a}、Dによる電位=\frac{Qx}{4πε_0a}$$これらをすべて加えたときの電位が0Vになるので$$\frac{Q}{4πε_0a}+\frac{-Q}{4πε_0a}+\frac{3Q}{4πε_0a}+\frac{Qx}{4πε_0a}=0$$$$Qx=-3Q$$となります。次に電界の大きさと向きについて考えます。

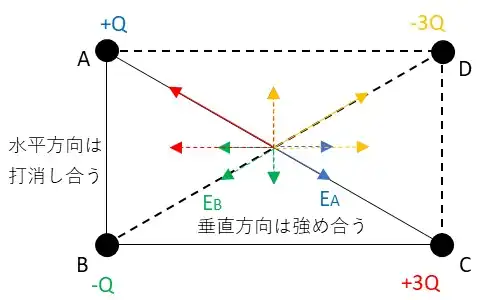
Aの電荷が作る電界について考えるとG点での電界はCの電荷に向かって進むような向きになります。これを水平方向と垂直方向に分けて考えたときのベクトル図はイラストの青い線のようになります。垂直方向は緑と被って見えています。

Bの電荷が作る電界について水平方向と垂直方向を考えると緑色の線のようになります。水平方向をみるとAの電荷が作る水平方向電界と同じ大きさで逆向きなのでお互いに打ち消しあいます。したがって垂直方向のみを考えればよいことになります。Cの電荷とDの電荷についても同様です。

Aと垂直方向の電界の大きさE_A1は$$E_{a1} = \frac{Q}{4πε_0a^2}sin30°= \frac{Q}{4πε_0a^2} × \frac{1}{2}$$となります。Bについても同様に計算できるのでAとBの電荷による垂直方向の電界の強さE_abは$$E_{ab} = E_{a1}×2 = \frac{Q}{4πε_0a^2}$$となります。

同様にしてCと垂直方向の電界の大きさE_c1は$$E_{a1} = \frac{3Q}{4πε_0a^2}sin30°= \frac{3Q}{4πε_0a^2}× \frac{1}{2}$$となります。Dについても同様に計算できるのでCとDの電荷による垂直方向の電界の強さE_cdは$$E_{cd} = E_{c1}×2 = \frac{3Q}{4πε_0a^2}$$となります。電界の大きさはE_allはE_cdとE_abの差となるので$$E_{all} = E_{cd} – E_{ab} = \frac{2Q}{4πε_0a^2}=\frac{Q}{2πε_0a^2}$$となりE_cdの方が大きいのでAからBに向かう向きと同じになります。従って④が正解となります。

R1年度の問題（電界とクーロン力）

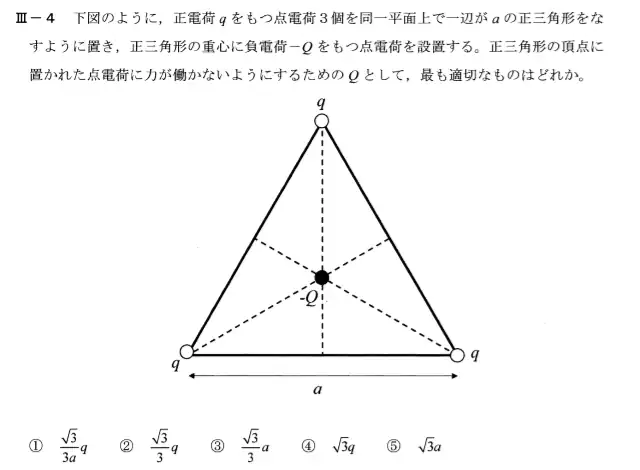
この問題のポイントは頂点A、B、Cそれぞれにお互いの電荷による力がかかっていることです。正三角形ですべての頂点の点電荷がｑで統一されているため点電荷の一つにかかるクーロン力を計算して基準とした点電荷のクーロン力を打ち消すQの値を考えることになります。

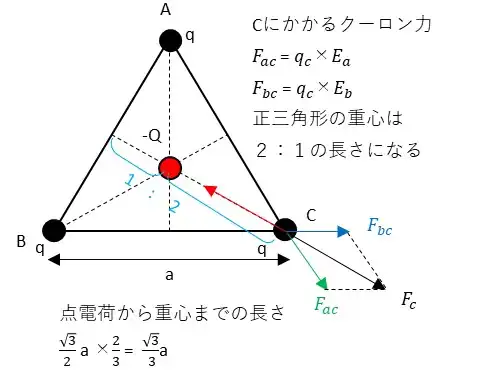
点電荷Cを基準にして考えます。点電荷Aと点電荷による電界は以下の通りです。
$$E_a = E_b =\frac{q}{4πε_0a^2}$$電界E_aと電界E_bによる点電荷にかかるクーロン力はF=QEより$$F_{ac} = F_{bc} =\frac{q×q}{4πε_0a^2}$$

クーロン力のベクトルを合成すると$$F_c =\frac{q×q}{4πε_0a^2}con30°×2＝\frac{q×q}{4πε_0a^2}×\frac{\sqrt{3}}{2}×2=\frac{\sqrt{3}q^2} {4πε_0a^2}$$次に点電荷Cの電界と正三角形の重心に置いた点電荷Qのクーロン力を考えます。重心までのクーロン力F_Gは$$F_G=\frac{Q×q}{4πε_0 (\frac{\sqrt{3}a}{3})^2}$$正三角形の頂点の点電荷に力がかからない条件はお互いの力が打ち消しあえばよいのでF_c＝F_Gとなります。

$$\frac{\sqrt{3}q^2} {4πε_0a^2} = \frac{Q×q}{4πε_0 (\frac{\sqrt{3}a}{3})^2}$$$$3Q = \sqrt{3}q $$$$Q=\frac{\sqrt{3}}{3}q$$従って②が正解となります。

点電荷の考え方

点電荷によるクーロン力と電界の関係について説明します。電界と電位の関係についても説明します。

電界とクーロン力の関係

電荷Q₀の近くに電荷Qを近づけるとクーロンの法則にしたがう電気力が働きます。電気力が働く空間を電界（電場）といいます。

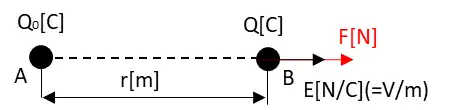
この電界を作っている点Aの点電荷Q₀[C]からr[m]離れた点Bに点電荷Q[C]をおくとこの点電荷に働く電気力Fは$$F=\frac{Q_0Q}{4πε_0r^2}$$となりクーロン力はFの方向になります。電荷Q[C]の受ける力Fは電荷Qに比例するのでQで割ると$$E=\frac{F}{Q}= \frac{Q_0}{4πε_0r^2}[V/m]・・（１）$$となります。

（１）は点Bの単位電荷あたりに働く電気力の大きさで、これをEで表して点Bでの電界の強さと定義しています。これを言い換えると電界Eの強さのところに電荷Q[C]の電荷をもってくるとF=EQ[N]の電気力が働くことになります。

電界と電位

電界中に置かれた電荷Q[C]を電界から受ける電気力に逆らって移動させるには仕事をする必要があります。

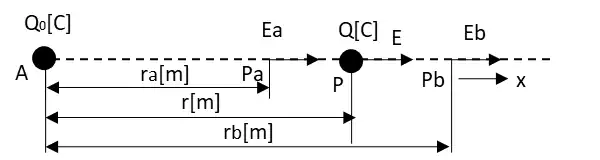
点P_bを無限遠点とすると無限遠点から点P_aまで電荷を移動させるために必要な仕事は$$W_a=\int_{∞}^{ra}-Fdr [J]$$となります。この式の両辺をQで割ると$$\frac{W_a}{Q}= \int_{∞}^{ra}-\frac{F}{Q}dr [\frac{J}{C}]$$となりF＝EQの関係から$$\frac{W_a}{Q}= \int_{∞}^{ra}-Edr [\frac{J}{C}]$$となります。

この式の意味は単位電荷あたりの仕事になります。無限遠点から電界内の点P_aまで単位正電荷を運ぶ仕事を点P_aの電位と定義しています。電位の単位は[J/C]ですが、これを[V]ボルトとしています。

したがって電位は$$V_a = \frac{W_a}{Q}= \int_{∞}^{ra}-Edr [V]$$となります。