【電気電子部門】技術士第一次試験の磁界中の起電力問題の解説

こんにちは、ENGかぴです。

技術士第一次試験の電気電子部門の試験においてに磁界中を動く導体の電流を求める計算問題が出題されています。フレミング右手の法則の考え方が分かっていれば簡単に計算することができます。過去に出題されている問題について解き方を記事にしました。

電流と磁界と電磁力の関係を示しているフレミング左手の法則についても説明していますので右手の法則との違いと考え方の参考になると思います。

技術士第一次試験の勉強におすすめする参考書や電気電子部門のポイント解説についてまとめています。これらのシリーズで2か月間勉強することで十分合格できます。

磁界中の導体が移動することによる起電力の問題
1. R2年度の問題
フレミング右手の法則
フレミング左手の法則
関連リンク

磁界中の導体が移動することによる起電力の問題

導体に電流を流すことで磁界が発生しお互いの導体に働く力に関する問題は過去数回出題されていましたが、R2年度では平等磁界中の導体が移動することによる誘導起電力から回路の電流を求める問題が出題されています。公開されている過去問を引用して説明していきます。

R2年度の問題

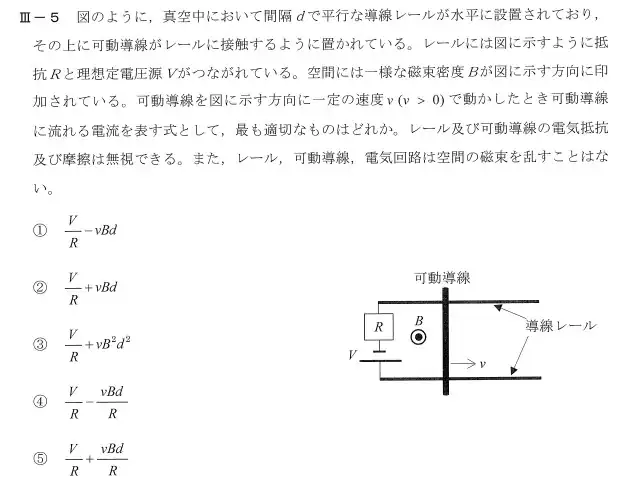
この問題のポイントはRに流れる電流が電源Vによるものと可動導線が磁界中を移動することによって発生する誘導起電力による電流の重ね合わせになることです。

電源Vによる電流はオームの法則から$I_V=V/R$になります。次に一様な磁界の中で可動導線をvの方向に動かしたときに発生する電流を求めます。導線レールの距離がdであるから可動導線の長さもdとなり電流が流れます。

磁束密度B[T]が一様でありその中を導体が速さv[m/s]でdt秒間動いたとすると磁束の変化は$$dΦ= Bd・vdt(Φ=BS )$$となります。誘導起電力の大きさはファラデーの法則から$$E = \frac{dΦ}{dt} = \frac{Bdvdt}{dt} = Bdv[V]$$となります。この誘導起電力による電流もRに流れるため誘導起電力による電流を求めると$$I_E = \frac{E}{R} = \frac{Bdv}{R}$$となります。この段階で正解は④と⑤になりますが、誘導起電力が電流を強める方なのか弱める方なのかの向きを考えると答えになります。

導体を一様な磁界の中で動かすとフレミング右手の法則により導体を動かす方向が分かれば誘導起電力の方向が分かります。

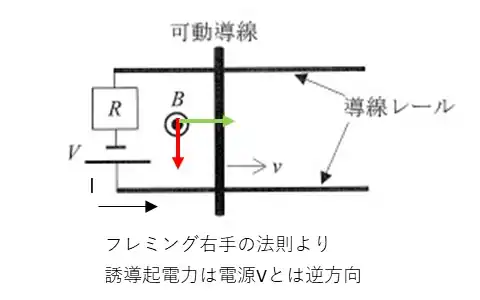
問題の図にフレミング右手の法則をあてはめます。磁束（磁界）の方向がB（紙面から上に向かう方向で人差し指）導体を動かす方向（親指）でvの方向になるので誘導起電力の方向（中指）は赤の矢印の方向になります。

これより導体を動かすことによって発生する誘導起電力の向きは電源Vと逆方向になることが分かります。

誘導起電力がVの逆向きの方向なので求める電流は$$I = I_V – I_E=\frac{V}{R}-\frac{vBd}{R}$$になります。従って正解は④になります。

フレミング右手の法則

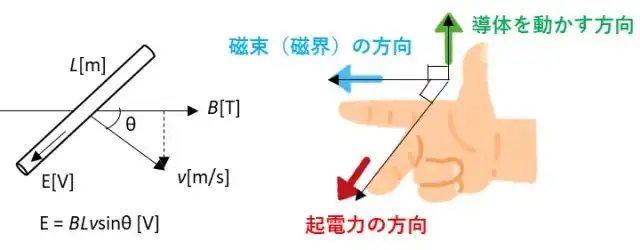
一様の磁界の中に導体を置き動かすと導体が磁束を切ることになるので電磁誘導から導体内に誘導起電力が発生します。磁界の向きが同一であった場合導体を動かす方向を逆にすると誘導起電力の向きも逆向きになります。

誘導起電力の大きさは導体が移動して磁束を切った分の変化を求めて電磁誘導に関するファラデーの法則によって求めることができます。

導体の長さをL[m]とし一様な磁束密度B[T]の磁界の中で導体を角度θをつけてv[m/s]でdt秒間動かしたとします。Bと鉛直成分がvsinθになるので磁束の変化dΦは以下のようになります。$$dΦ = BL・vsinθdt[Wb]・・(1)$$となりファラデーの法則を適用すると$$E = \frac{dΦ}{dt}= \frac{BLvsinθdt}{dt} = BLvsinθ[V]・・(2)$$となります。

フレミング右手の法則は導体の動く方向（親指）、磁界の方向（人差し指）、誘導起電力の方向（中指）がイラストのように直角に開いた状態の方向となることを示したものです。

フレミング左手の法則

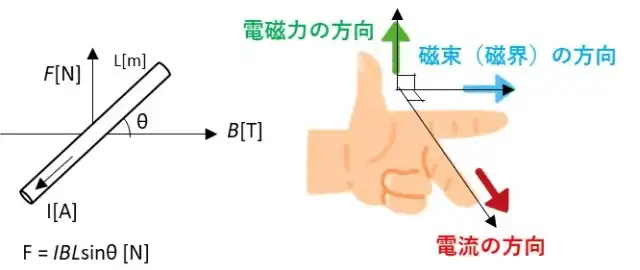
導体に電流が流れるとアンペアの右ねじの法則に従った磁界が発生します。この磁界を囲うように他の磁石や導線によって他の磁界ができると電流と磁界の間に電磁力が働きます。

他の磁界と導体に流れた電流による磁界が合成された磁界によって磁界が強い方から弱い方に向けて電磁力を受けることになります。

フレミング左手の法則は磁界の方向に垂直に電流を流すと導体に加わる電磁力（親指）、磁界の方向（人差し指）、電流の方向（中指）がイラストのように直角に開いた状態の方向となることを示したものです。

電磁力の強さは、アンペアの実験によって以下のように定義されています。$$F = IBLsinθ[N]・・(3)$$

θは磁界の向きと電流方向とのなす角で磁界に対して垂直成分をとるためsinθとなっています。フレミング左手の法則によって電磁力の向きを考える例として、2本の平行導体がお互いに与え合う力について考えてみます。

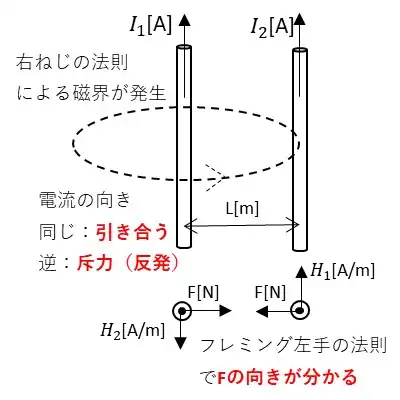
電流が流れている2本の導体にはお互いの電流によって発生した磁界によって電磁力が働きます。この電磁力の向きはフレミング左手の法則による向きになります。2本の導線の長さをｄ[m]とします。

電流I₁によってL[m]離れた点の磁界の大きさはアンペアの法則より$$H_1 = \frac{I_1}{2πL}[A/m]$$となります。

また磁束密度はB₁=μH₁[T]なので導線に働く電磁力は式(3)より$$F = I_2μH_1×d×sin90° = \frac{μI_1I_2d}{2πL}[N]$$になります。電流I₂による電磁力も同様にして求めることができますが、電磁力の大きさは同じになります。電磁力を求めた後は、フレミング左手の法則に当てはめてることで電磁力の向きが分かります。

並行導線の電流間に働く電磁力の向き：
同じ方向に電流を流すと引き合い、逆の方向に電流を流すと斥力（反発）します。