こんにちは、ENGかぴです。
技術士第一次試験の電気電子部門の試験においてに交流回路の共振周波数から共振の鋭さを求める問題や共振周波数からコンデンサ容量を求める計算問題が出題されています。交流回路のインピーダンスから共振する条件が分かっていれば難しくありません。
交流回路のリアクタンスから容量性負荷であるかもしくは誘導性負荷であるかの判断についてや共振した際の共振の鋭さに関してまとめていますので参考になると思います。
技術士第一次試験の勉強におすすめする参考書や電気電子部門のポイント解説についてまとめています。これらのシリーズで2か月間勉強することで十分合格できます。
【電気電子部門】技術士第一次試験の勉強におすすめの参考書3選
交流回路の共振に関する問題
交流回路ではコンデンサやコイルが周波数によってインピーダンスを変化しながら動作します。交流回路では虚数部分によって容量性に働くか誘導性に働くかが決まります。R2年度では交流回路の直列接続と並列接続に関して共振している条件から共振の鋭さやコンデンサの容量を計算する問題が出題されています。公開されている過去問を引用して説明していきます。
R2年度の問題(直列回路)
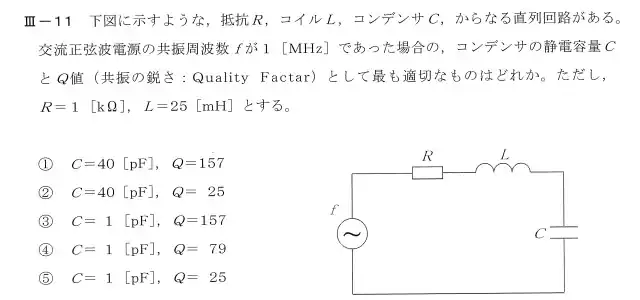
この問題のポイントは交流回路においてインピーダンスを求めた時の虚数部分が共振によって0になっていることや共振の鋭さQが共振時のコンデンサとコイル間の電圧をQ倍する係数であることが分かっているかです。
交流正弦波電源において直列回路のインピーダンスは、$$Z=R+j(ωL+\frac{1}{ωC})$$となります。共振時は虚数部が0になるので$$ωL-\frac{1}{ωC}=0$$$$ω^2 = \frac{1}{LC}$$$$f=\frac{1}{2π\sqrt{LC}}[Hz]$$となります。この時のfが共振周波数となります。共振周波数が1[MHz]であることからコンデンサの容量を求めます。fの式をCの式に変換して求めると$$C=\frac{1}{(2πf)^2L}= \frac{1}{(2π1×10^6)^2×25×10^{-3}}=1.0[pF]$$となります。
交流回路の電圧をEとすると共振時に回路に流れる電流は虚数部が0であるから\(I=\frac{E}{R}\)となりコンデンサ及びコイル両端の電圧は以下のようになります。$$E_L=ωLI=\frac{ωL}{R}E、E_C=\frac{1}{ωC}\frac{E}{R}=\frac{1}{ωCR}E$$になります。共振時のEを係数倍してるものがQなので$$Q=\frac{ωL}{R}=\frac{1}{ωCR}$$になります。Qを求めると$$Q=\frac{ωL}{R}=\frac{2π×25×10^{-3}}{1×10^3}=157$$となります。従って、③が正解になります。
PR:スキマ時間で自己啓発!スマホで学べる人気のオンライン資格講座【スタディング】まずは気になる講座を無料で体験しよう!
R2年度の問題(並列回路)
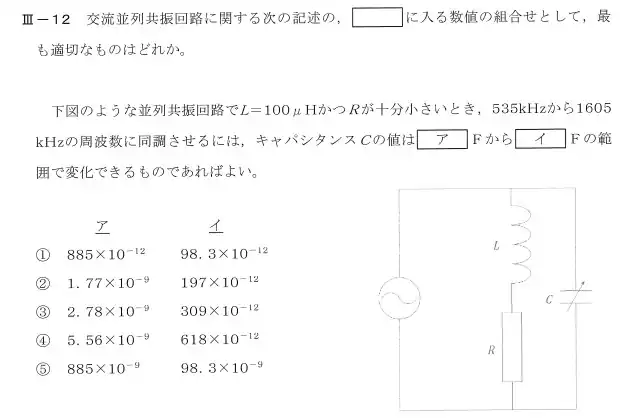
この問題のポイントは回路のインピーダンス(アドミタンス)を求めて虚数部分が0になる条件からコンデンサの値を算出します。
並列回路なのでインピーダンスを求めるよりその逆数であるアドミタンスで考えた方が楽です。アドミタンスであっても虚数部分が0になる条件を求めればよいのでアドミタンスで考えます。$$Y=Z^{-1}=\frac{1}{R+jωL}+jωC$$$$=\frac{R+j(-ωL+ωCR^2-ωC(ωL)^2)}{R^2+(ωL)^2}$$となります。虚数部分が0となる条件が共振周波数なので$$-ωL+ωCR^2+ωC(ωL)^2=0$$ここで問題にも記載されているRが十分に小さい時という条件からRを二乗している項は値が小さくなることから0とみなせば$$-ωL+ωC(ωL)^2=0$$$$C=\frac{1}{ω^2L}[F]$$となります。この式に共振周波数fの最小値と最大値を代入して範囲を求めます。$$C_{min}=\frac{1}{(2π×535×10^3×100×10^{-6})^2}= 885×10^{-12}[F]$$$$C_{max}=\frac{1}{(2π×1605×10^3×100×10^{-6})^2}= 98.3×10^{-12}[F]$$となります。従って正解は①になります。
PR:スキマ時間で自己啓発!スマホで学べる人気のオンライン資格講座【スタディング】まずは気になる講座を無料で体験しよう!
交流回路の共振について
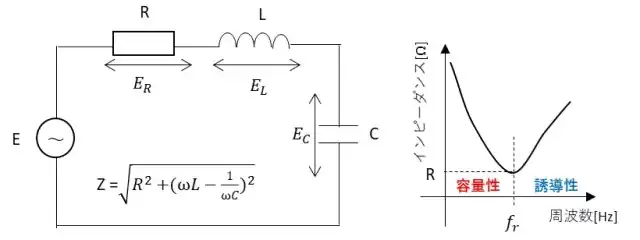
交流回路の共振について直列回路のもとに周波数特性を考えていきます。共振の条件は虚数部分が0になることなのでこの考え方は並列回路でも同様に使用できます。
インピーダンスの大きさは$$Z=\sqrt{R^2+(ωL-\frac{1}{ωC})^2}$$となります。コンデンサとコイルのリアクタンスについて周波数を変化させたときの変化を考えます。コイルによる誘導リアクタンスXLはXL=ωLから周波数に対して比例の関係となりコンデンサによる容量リアクタンスはXC=1/ωCから周波数に反比例します。
この関係からインピーダンスの周波数特性を示すと周波数ーインピーダンスの図のようになります。インピーダンスが最も低くなる周波数ではインピーダンスはR[Ω]となり、この時の周波数を共振周波数といいます。
共振周波数は誘導リアクタンスと容量リアクタンスが一致する点であるためリアクタンス分が0になる条件から求めることができます。共振周波数frは$$ωL-\frac{1}{ωC}=0$$$$f_r = \frac{1}{2π\sqrt{LC}}[Hz]$$となります。
インピーダンスが最小ということは、回路において最大電力が取り出せる条件と言い換えることもできますのでインピーダンスマッチングで最大電力を取り出す条件でもあります。
共振周波数よりも低い周波数の場合はリアクタンス分でXC>XLとなるため容量性の回路となり共振周波数よりも高い場合はリアクタンス分でXL>XCとなるため誘導性の回路となります。
共振しているときの電流IrはIr=E/R[A]となりこの時のLやC両端の電圧EL及びECはオームの法則を適用して$$E_L=ωLI_r =\frac{ωL}{R}E[V]・・(1)$$$$E_C=\frac{1}{ωC}I_r=\frac{1}{ωCR}E[V]・・(2)$$となり共振時はELとECは一致しているためEL=ECとなります。この時のELとECを共振の鋭さQとして定義しています。
共振の鋭さであるQは共振時のコイルとコンデンサの電圧に対する係数であり共振時の回路の良さを示す目安になります。
$$Q=\frac{ωL}{R}=\frac{1}{ωCR}・・(3)$$であり共振時の電圧は(1)(2)を(3)を使って示すと$$E_L=QE[V]、E_C=QE[V]$$になります。
関連リンク
関連するリンクでは技術士第一次試験の勉強におすすめする参考書や電気電子部門のポイント解説についてまとめています。
PR:わからないを放置せず、あなたにあった最低限のスキルを身に着けるコツを教える テックジム 「書けるが先で、理解が後」を体験しよう!
最後まで、読んでいただきありがとうございました。