【電気電子部門】技術士第一次試験の電動機に関する問題の解説

こんにちは、ENGかぴです。

技術士第一次試験の電気電子部門の試験においてに電動機に関する計算問題が出題されています。同期速度と周波数と極数の関係が分かっていれば簡単に計算することができます。電動機の滑りに関する考え方についてもまとめています。

技術士第一次試験の勉強におすすめする参考書や電気電子部門のポイント解説についてまとめています。これらのシリーズで2か月間勉強することで十分合格できます。

【電気電子部門】技術士第一次試験の勉強におすすめの参考書3選

電動機に関する問題
1. R1年度（再試験）の問題
2. H29年度の問題
電動機の滑りの考え方
1. 同期速度と滑り
2. トルクの比例推移
関連リンク

電動機に関する問題

電動機に関する問題と電動機の滑りに関する問題の出題頻度は数年に一度とそこまで多くはないのですが、考え方が分かっていれば簡単に解くことができます。公開されている過去問を引用して説明していきます。

R1年度（再試験）の問題

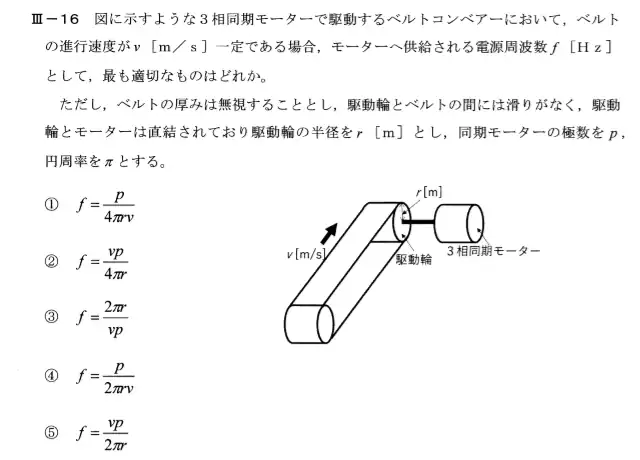
この問題のポイントは、同期速度と周波数と極数の関係が分かっているかになります。

同期モータの回転磁界の回転速度は2極の巻線で1サイクルで1回転します。一般に極数をp、周波数f [Hz]とすると、回転磁界の回転速度N_s[s‾¹]は$$N_s=\frac{2f}{p}[min^{-1}] = \frac{120f}{p}[s^{-1}]$$となります。この回転速度は同期速度と言われており回転磁界は負荷に関係なく同期速度で回転します。

ベルトの速度がv[m/s]であり駆動期の半径がr[m]であるから駆動機の円周の長さ2πrにおいて1秒当たりの回転数Nは$N= \frac{V}{2πr}[s^{-1}]$になります。滑りがない条件からN_s=Nになるので$$\frac{v}{2πr} = \frac{2f}{p}$$ $$ f= \frac{vp}{4πr}[Hz]$$となります。したがって②が正解になります。

H29年度の問題

この問題のポイントは、同期速度を求めて970[min^-1]になるときの滑りを求めて挿入抵抗の滑りの関係をトルクの比例推移から求めていきます。

トルクの比例推移とは滑りsの時のトルクがsの多いほうに回転子抵抗に比例して移動することを言います。詳細は下記のトルクの比例推移を参照ください。

電動機の同期速度N_sは$$N_s = \frac{2f}{p} = \frac{120×50}{6} = 1000[min^{-1}]$$になります。滑りは同期速度に対する回転数の割合なので回転速度970[min^-1]の時の滑りs₁は$$s_1 = \frac{1000 – 970}{1000} = 0.03 = 4 [％]$$になります。

比例推移の考え方からRを一相に接続する抵抗とすると、同一トルクが得られる時の滑りと2次抵抗の関係は下のようになります。$$\frac{r}{s} = \frac{r + R}{s_1}$$

rが2次巻線の各相の抵抗値、s₁は抵抗挿入後の滑り、ｓは変化する前の滑りです。この関係から$$\frac{0.2}{2} = \frac{0.2 + R}{3} $$$$R = 0.1[Ω]$$となります。したがって①が正解になります。

電動機の滑りの考え方

電動機の同期速度と滑りの考え方についてまとめました。公式を覚えておけば対応できると思います。

同期速度と滑り

回転磁界の回転速度は一般に極数をｐ、周波数f[Hz]とすると回転磁界の回転速度は以下の式になります。

$$N_s = \frac{2f}{p}[s^{-1}] = \frac{120f}{p}[min^{-1}]・・(1)$$となります。この速度は同期速度といい、回転磁界は負荷に関係なく同期速度で回転します。

電動機の回転子導体は、同期速度の回転磁界に追い越されることで磁束を切り回転し内に起電力が生じることで回転磁界と磁束の間に回転力（トルク）を発生します。そのため同期速度よりも必ず遅れて回転することになります。

滑りは回転子が同期速度よりも遅く回転する差の割合であり回転子の速度N[min^-1]、同期速度N_s[min^-1]とすると以下の関係式が得られます。

$$s = \frac{N_s – N}{N_s}・・(2) 、s = \frac{N_s – N}{N_s}×100[％] ・・(3)$$ $$ N = N_s(1 – s )= \frac{120f}{p}(1 – s)[min^{-1}]・・(4)$$

定格負荷時の滑りは電動機の出力容量が大きくなるにつれて小さくなります。

トルクの比例推移

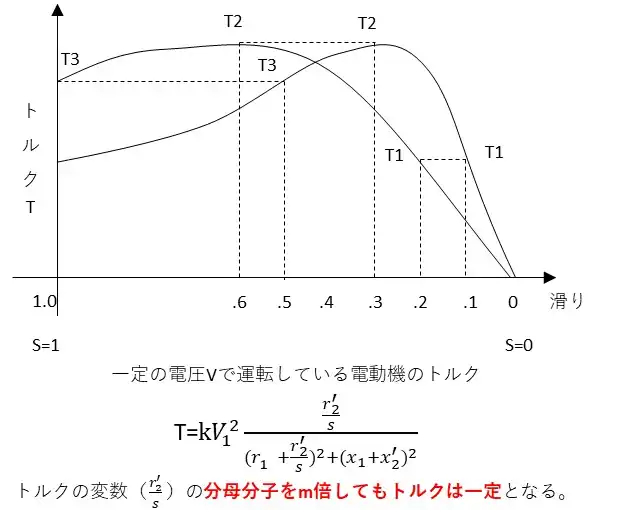
一定の電圧Vで運転している電動機のトルクはイラストの式で表されます。この式の中でも可変となるのは滑りを含む$\frac{r_2^{‘}}{s}$の部分です。次に、この部分をm倍したとすると$$\frac{mr_2^{‘}}{ms} = \frac{r_2^{‘}}{s}$$となります。回転子の抵抗を2倍にしたとすると、s=0.1のトルクT1はs=0.2のところに、s=0.3のトルクT2は0.3×2=0.6というようにｓが増えていく方向に回転子抵抗に比例して移動します。これをトルクの比例推移といいます。

回転子の抵抗r₂’（二次抵抗）の変化による電動機の特性についてまとめると