こんにちは、ENGかぴです。
技術士第一次試験の電気電子部門の試験においてにオペアンプ関する計算問題が出題されています。オールパスフィルタが出題されていますが、考え方が分かっていれば簡単に計算することができます。反転増幅器と非反転増幅器考え方についてもまとめています。
技術士第一次試験の勉強におすすめする参考書や電気電子部門のポイント解説についてまとめています。これらのシリーズで2か月間勉強することで十分合格できます。
【電気電子部門】技術士第一次試験の勉強におすすめの参考書3選
オペアンプに関する問題
オペアンプに関する問題の出題頻度は多いと思います。考え方が分かっていれば簡単に解くことができます。非反転増幅回路と反転増幅回路の双方の知識が必要となるオールパス回路について、公開されている過去問を引用して説明していきます。
R1（再試験）年度の問題
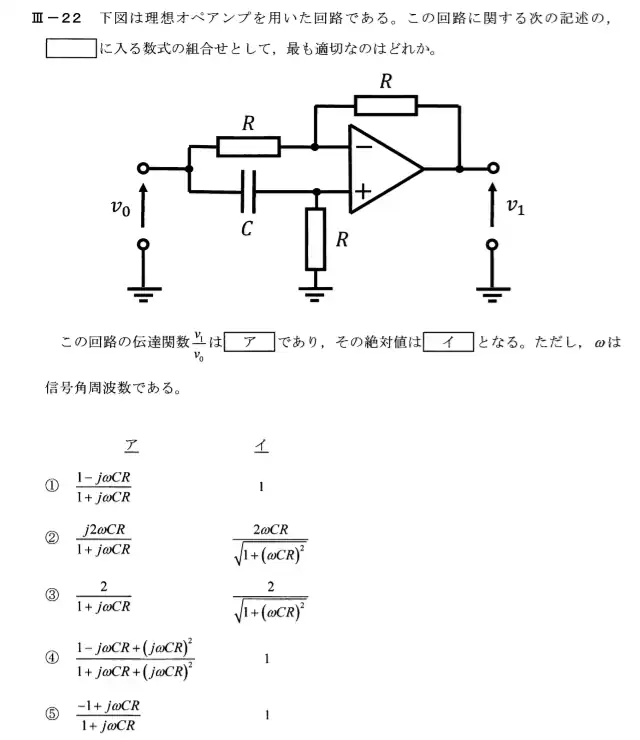
この問題のポイントは、オペアンプのプラス側とマイナス側に異なる電圧が印加されていることです。プラス側から見たときは非反転増幅回路となりマイナス側から見たときには反転増幅回路になることです。出力電圧はこれらの出力の合成で考えることができます。
プラス側を基準にして考えます。プラス端子に印加される電圧VO+は$$V_{0+} = \frac{R}{\frac{1}{jωC}+R}V_0 = \frac{jωCR}{1+jωCR}V_0$$プラス端子にこの電圧が印加された状態で非反転増幅されるのでプラス側を基準にしたときの出力電圧V1+は$$V_{1+} = (1 + \frac{R}{R})V_{0+}= \frac{2jωCR}{1+jωCR}V_0$$となります。次にマイナス側を基準にして考えます。マイナス端子にはVoがRの比率からゲインをもって反転増幅されるのでマイナス側を基準にしたときの出力電圧V1-は$$V_{1-} = -\frac{R}{R}V_0 = -V_0$$となります。出力電圧V1はこれらの電圧を重ね合わせた合成なので$$V_1 = V_{1+} + V_{1-} = \frac{2jωCR}{1+jωCR}V_0 – V_0 = \frac{-1 + jωCR}{1 + jωCR}V_0$$したがって、伝達関数は$$\frac{V_1}{V_0} = \frac{-1 + jωCR}{1 + jωCR}$$となり絶対値は$$|\frac{V_1}{V_0}| = \frac{\sqrt{(-1)^2 + (ωCR)^2}}{\sqrt{(1)^2 + (ωCR^2)}} = 1$$となります。したがって⑤が正解になります。
H30年度の問題
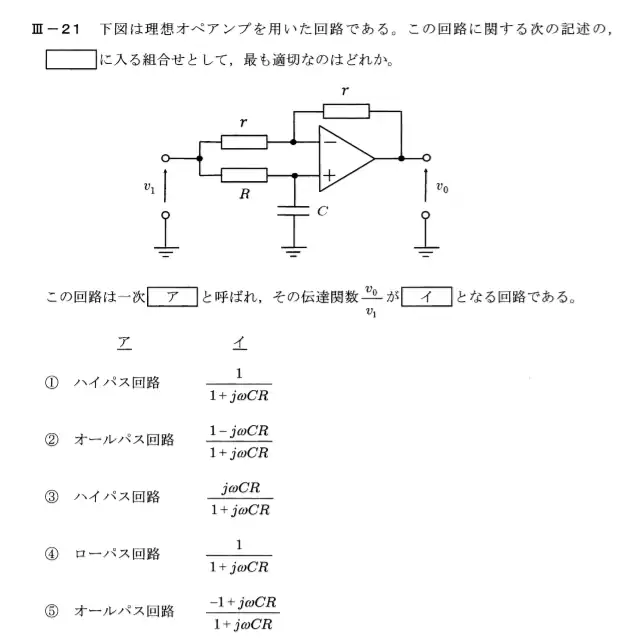
この問題のポイントは、R1年度（再試験）と同じですが、回路名称としてオールパス回路（移相器）と呼ばれていることです。これが分かっているだけで2択問題になります。この問題もプラス側とマイナス側に分けて出力電圧を計算し、合成することで求めることができます。
プラス側を基準にして考えます。プラス端子に印加される電圧Vo+は$$V_{0+} = \frac{\frac{1}{jωC}}{R + \frac{1}{jωC}}V_0 = \frac{1}{1+jωCR}V_0$$プラス端子にこの電圧が印加された状態で非反転増幅されるのでプラス側を基準にしたときの出力電圧V1+は$$V_{1+} = (1 + \frac{r}{r})V_{0+}= \frac{2}{1+jωCR}V_0$$となります。次にマイナス側を基準にして考えます。マイナス端子にはVoがrの比率からゲインをもって反転増幅されるのでマイナス側を基準にしたときの出力電圧V1-は$$V_{1-} = -\frac{r}{r}V_0 = -V_0$$となります。出力電圧V1はこれらの電圧を重ね合わせた合成なので$$V_1 = V_{1+} + V_{1-} = \frac{2}{1+jωCR}V_0 – V_0 = \frac{1 – jωCR}{1 + jωCR}V_0$$したがって、伝達関数は$$\frac{V_1}{V_0} = \frac{1 – jωCR}{1 + jωCR}$$したがって②が正解になります。
広告
別の解放（キルヒホッフの法則）・・解法追記
上記のように重ね合わせの理を使用する方法もありますが、キルヒホッフの第2法則である電流の法則を使用して考えると、この問題の場合はシンプルに考えることができます。
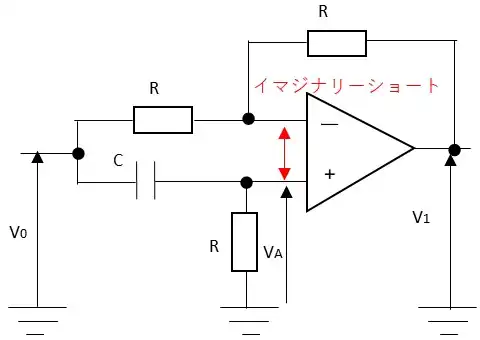
オペアンプのプラス端子とマイナス端子はイマジナリーショートとみなさせるのでこの電圧をVAと置くとマイナス端子に流れ込む電流は$$\frac{V_0-V_A}{R}+\frac{V_1-V_A}{R} = 0・・（A）$$となります。プラス端子に流れ込む電流は$$\frac{V_0-V_1}{\frac{1}{jωC}}-\frac{V_A}{R} = 0・・（B）$$となります。式（A)から$$V_A=\frac{V_1+V_0}{2}$$となるので式（B)に代入すると$$jωC(V_1-\frac{V_1+V_0}{2})-\frac{V_1+V_0}{R} = 0$$ $$V_0=\frac{jωCR-1}{jωCR+1}V_1$$となります。
オペアンプ（オールパス回路）の考え方
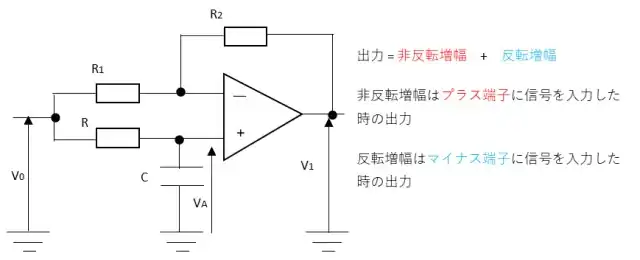
オペアンプを使って位相器を作ることができ、この回路はオールパス回路と呼ばれています。出力はプラス端子とマイナス端子に印加された電圧が周辺の抵抗によってゲインを持つようになります。
プラス端子とマイナス端子それぞれを基準にして非反転増幅回路と反転増幅回路からそれぞれの出力電圧をもとめて、合成したものが出力電圧となります。
したがって、出力電圧V1は
$$V_1 = (1 + \frac{R_2}{R_1})V_A – \frac{R_2}{R_1}V_0$$
となります。VAはRとCを分圧した電圧になります。位相器として使用されているイメージを見てみるためシミュレーションした結果が以下になります。
入力には波高値が1VになるAC波形を印加しています。この時の出力電圧をシミュレーションすると、出力電圧OUT（黄色）は入力電圧IN（緑色）よりも位相が遅れて出力されていることが分かります。位相はCRの乗数で決まります。
広告
非反転増幅回路
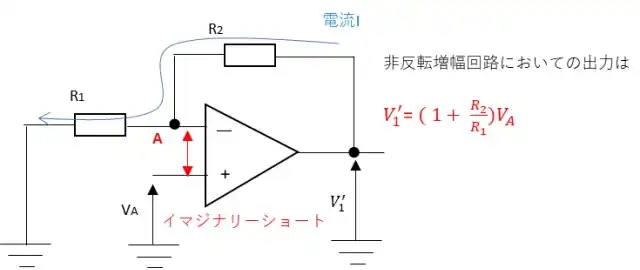
オペアンプの入力ピンのインピーダンスは無限大とみなせるためイマジナリーショートからA点の電圧はVAとなります。電流Iはオペアンプには流れないのでR1とR2に流れます。このことから$$V_A = R_1I・・(1)$$ $$V_1^{’}= (R_1 + R_2)I・・(2)$$となります。(1)より$$I = \frac{V_A}{R_1}$$となるから(1)に代入すると
$$V_1^{’}= ( R_1 + R_2 )\frac{V_A}{R_1} = ( 1 + \frac{R_2}{R_1})V_A$$
となります。
反転増幅回路
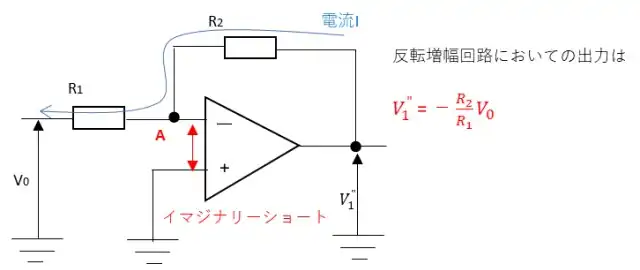
オペアンプの入力ピンのインピーダンスは無限大とみなせるためイマジナリーショートからA点の電圧は0となります。電流Iはオペアンプには流れないのでR1とR2に流れます。このことから$$V_0 = -R_1I・・(3)$$ $$V_1^{”}= R_2I・・(4)$$となります。(3)より$$I = -\frac{V_0}{R_1}$$となるから(4)に代入すると
$$V_1^{”} = -\frac{R_2}{R_1}V_0$$
となります。
関連リンク
関連するリンクでは技術士第一次試験の勉強におすすめする参考書や電気電子部門のポイント解説についてまとめています。興味があればご覧ください。
PR：わからないを放置せず、あなたにあった最低限のスキルを身に着けるコツを教える テックジム 「書けるが先で、理解が後」を体験しよう！
最後まで、読んでいただきありがとうございました。
重ね合わせの理による解き方よりもキルヒホッフの法則による解き方の方が簡単な場合があります。オペアンプの問題はイマジナリーショートからプラス端子とマイナス端子に流れ込む電流を考えるほうが簡単な場合があります。解きやすさから使い分けると良いと思います。