こんにちは、ENGかぴです。
エナジーハーベスト電源を測定しようとテスターを使ったところ負荷への電流が不足してしまうケースがありました。テスターのレンジの切り替えによって負荷への電流が不足したことが原因だったようです。
エナジーハーベストのように微小な電流を扱う場合テスターの内部抵抗やレンジの切り替えによって正確に電流計測できないことや測定方法によっては誤差が大きくなったことから電流計と電圧計の配線方法の違いによる測定誤差についてまとめました。
テスターの計測範囲切り替えによる誤差
普段回路のチェックのために電流や電圧をテスターを使いますが、エナジーハーベストのような微小電流を図るためにアナログテスターを使用していました。アナログテスターの計測範囲を切り替えることで測定ができたりできなかったりとしていました。
デジタルテスターにおいても電流のレンジを切り替えると負荷(IoTモジュール)への電源が安定しなくなったことからエナジーハーベストの消費電流の測定をする際はテスターの内部抵抗について考慮することがかなり重要であることが分かりました。
テスターの計測範囲の切り替えについて倍率器と分流器の原理を見てみます。
PR:外資系・IT業界などハイクラスの転職に強い【AXIS Agent】
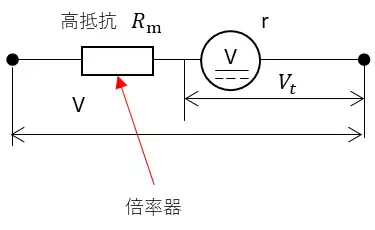
倍率器の原理
$$V=\frac{R_m+r}{r}V_t=(1+\frac{R_m}{r}V_t)=mV_t$$となります。テスターの値に対してm倍の電圧を測定することができます。
$$m=1+\frac{R_m}{r} = \frac{V}{V_t}$$となり、このmを倍率器としています。
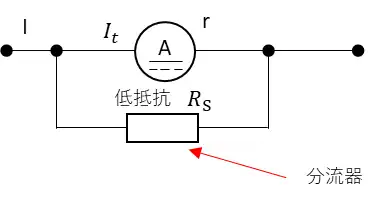
分流器の原理
$$I=\frac{r+R_S}{R_S}I_a = (1+\frac{r}{R_S}I_a) = nI_a$$となります。テスターの値に対してn倍の電流を測定することができます。
$$n = 1+ \frac{r}{R_S} = \frac{I}{I_a}$$となり、このnを分流器としています。
電流計から電圧系と電流計を作ってみる
電流計と電圧計は電流計から構成されています。つまり電流計から電圧計を作ることもできます。200uAの測定範囲で内部抵抗が100Ωの電流計から電圧計と電流計を作る例を上げます。
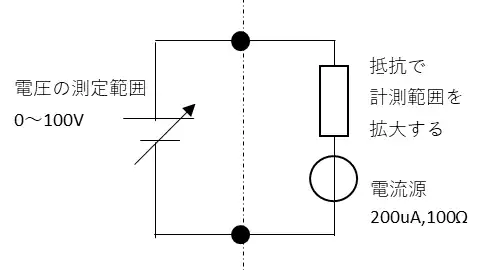
例)100Vの測定範囲となる電圧計をつくる
追加する抵抗をR[Ω]とすると最大電圧である100Vとしたときオームの法則から以下のようになります。$$100 = ( R + 100 )×200×10^{-6}$$
$$R = 499900[Ω]≒500[kΩ] $$となります。倍率器として500kΩの抵抗を追加することで100Vまで計測できる電圧計を作ることができます。
PR:スキマ時間で自己啓発!スマホで学べる人気のオンライン資格講座【スタディング】まずは気になる講座を無料で体験しよう!
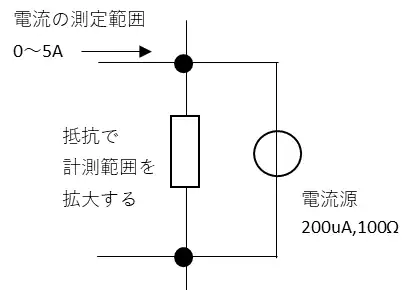
例)5Aの測定範囲となる電流計を作る
抵抗を電流源(電流計)に並列になるように接続します。抵抗の間の電圧は電流源に印加される電圧と同じなので$$V = 200×10^{-6}×100 = 2 ×10^{-4}[V]$$となります。
追加した抵抗に流れる電流は最大電流の5Aから電流源分を引いた分なので4.9998[A]になります。求める抵抗は$$R = \frac{2×10^{-4}}{4.9998}≒4×10^{-3}[Ω]$$となります。分流器として4[mΩ]の抵抗を追加することで5Aまで計測できる電流計を作ることができます。
電流計の抵抗値はかなり小さくなるため電流のレンジで間違って電圧を図ってしまうと瞬時に大きな電流が流れてしまうためヒューズが切れて測定できなくなってしまうことがあります。
PR:エンジニア転職なら100%自社内開発求人に強い【クラウドリンク】
抵抗の測定方法による誤差
電気回路の抵抗(インピーダンス)を測定するために電流計と電圧計を使って簡易的に抵抗測定する方法があります。テスターの値からオームの法則に従って抵抗を計算します。$$R = \frac{E}{I}=\frac{電圧計の値}{電流計の値}[Ω]$$
オームの法則に従って抵抗値を算出しますがテスタ2つの配線方法での測定を考えてみます。
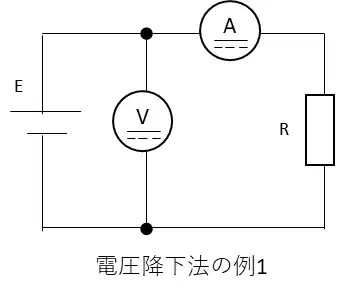
電圧降下法1の場合は電流計の内部抵抗が誤差として表れるためテスターの値から抵抗を計算した後で電流計の内部抵抗Raを差し引いて補正します。
$$R=\frac{E}{I}-R_a[Ω]$$として抵抗値を補正します。
電流計の内部抵抗は小さいことを考えると負荷の抵抗が大きく誤差が気にならない場合に有効な配線となります。
電圧計の内部抵抗は比較的大きいので電圧計に流れる電流が省略できる範囲の抵抗の測定に有効です。デジタル電圧計は内部インピーダンスが高いことが多いので比較的小さな抵抗を測定するのに有効な配線となります。
これらの方法による抵抗の測定は電圧降下法による測定方法になります。
PR:(即戦力のスキルを身に着ける:DMM WEBCAMP 学習コース(はじめてのプログラミングコース))
電力計測の誤差
電圧降下法の2例から電力を測定したときの誤差について考えてみます。電圧計と電流計の接続方法には抵抗の測定方法による誤差で説明した2通りがあります。測定器の内部抵抗や負荷の大きさの関係から誤差の少ない測定方法を選択すると良いでしょう。
電力量を計算してどちらの配線が誤差が少なくなるかを考えてみます。
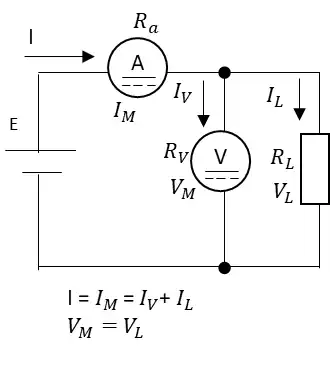
回路1の電力量の誤差について計算します。真の電力は$$P=V_LI_L$$$$=(V_M-V_a)IL$$$$=(V_MI_L -I_L^2R_a)$$$$=P_1-I_L^2R_a$$となります。電流計の内部抵抗のRaにより\(I_L^2R_a\)だけ誤差が出ることを示しています。
回路1について\(P=V_LI_L=R_LI_L^2 \)の関係から誤差率を求めます。
$$ε_1 = \frac{P_1-P}{P}=\frac{1}{P}(I_L^2R_a)=\frac{R_a}{R_L}$$となります。
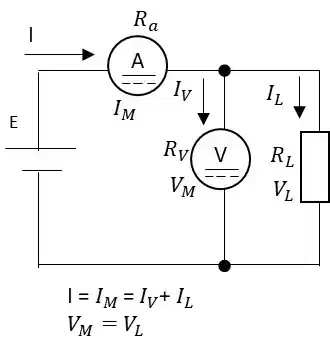
回路2の電力量の誤差について計算します。真の電力は$$P=V_LI_L$$$$=V_L(I-I_V)$$$$=V_LI-\frac{V_L^2}{R_V}$$$$=P_2-\frac{V_L^2}{R_v}$$電圧計の内部抵抗のRVにより\(\frac{V_L^2}{R_V}\)だけ誤差が出ることを示しています。
回路2について\(P=V_LI_L=\frac{V_L^2}{R_L} \)の関係から誤差率を求めます。
$$ε_2 = \frac{P_2-P}{P}=\frac{1}{P}(\frac{V_L^2}{R_V})=\frac{R_L}{R_a}$$となります。
回路1と回路2の結果の差を取り接続法の誤差について考えます。
$$ε_1-ε_2=\frac{R_a}{R_L}-\frac{R_L}{R_a}=\frac{R_aR_L-R_L^2}{R_VR_L}$$となります。
\(R_aR_L-R_L^2 >0\)であれば回路2・・(1)
\(R_aR_L-R_L^2 <0\)であれば回路1・・(2)
が誤差が少ない測定方法となります。一般的に電流計の内部抵抗Raは小さく電圧計の内部抵抗RVは大きいので負荷抵抗の大きさがある程度把握できれば測定方法を選択することで精度よく測定できるようになります。
例)電流計の内部抵抗が0.2[Ω]、電圧計の内部抵抗が100[kΩ]のとき負荷抵抗が200[Ω]の場合の接続の場合
\(R_aR_V = 0.2×100×10^3 = 2×10^4\)であり、\(R_L^2=4×10^4\)となるので(2)の条件となるので回路1の方が測定方法として良いことになります。
関連リンク
エナジーハーベストの実験においてテスターの動作からテスターの誤差について考えてみました。エナジーハーベストにおいて消費電力を測定する際はテスターの選択についても考慮する必要があります。
エナジーハーベストについて実験したことについて下記リンクでまとめています。興味があればご覧ください。
最後まで、読んでいただきありがとうございました。