こんにちは、ENGかぴです。
方形波/三角波発振回路はオペアンプの基本回路である積分回路とコンパレータによって構成されます。ファンクションジェネレータとも呼ばれており各種様々な波形を生成する基礎にもなっています。これらの回路の用途や特徴について解説しています。
下記リンクではオペアンプで押さえておきたい基本特性と基本回路や私が経験してきたオペアンプの応用回路に関するリンクをまとめています。
ルネサスエレクトロニクスのUPC258G2をもとにシミュレーションを行っています。また産業用の機器のアナログ回路を対象としており入力電圧の周波数は50Hz(60Hz)をベースにしています。
方形波/三角波発振回路
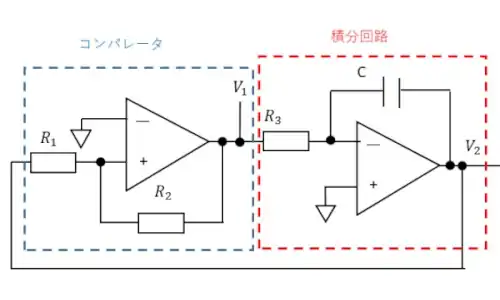
この回路はシュミット回路と積分回路を組み合わせたもので、ファンクションジェネレータと言われています。コンパレータの出力で積分コンデンサを充電と放電することで三角波が生成できます。
コンパレータ出力V1は方形波で振幅はオペアンプのVH-VLで決まります。積分回路の出力V2は三角波で振幅はヒステリシス幅R1(VH-VL)/R2となります。発振周波数fは$$f=\frac{R_2}{4CR_1R_3}・・(1)$$となります。
動作原理
初期条件としてt=0、V2=0Vとします。①の電圧は②と③の電圧差を抵抗R1とR2で分割した値です。シュミット回路の出力電圧+V1をT間積分してV2になったとします。$$-\frac{1}{CR_3}\int_0^TV_1dt = V_2・・(2)$$ $$V_1-\frac{R_2}{R_1+R_2}(V_1-V_2)≦0・・(3)$$となります。式(3)を満たすとき出力が反転します。式(2)から$$V_2=-\frac{T}{CR_3}V_1・・(4)$$ 式(4)を式(3)に代入してTを求めると$$T=CR_3(\frac{R_1}{R_2})$$となります。この式を式(2)に代入すると$$V_2=-(\frac{R_1}{R_2})V1・・(5)$$となります。式(5)がV2の最小値になります。V2は式(3)の条件を満たすと反転して-V1になります。積分器はこの-V1を積分することになり出力電圧V2は(5)を初期値として積分するので$$V_2=-(\frac{R_1}{R_2}V_1)-\frac{1}{CR_3}\int_0^{\frac{T}{2}}(-V_1)dt・・(6)$$となります。-V1から+V1までの周期はT/2となるのでこの区間積分することになります。積分により①の電圧が大きくなっていき$$(-V_1)-\frac{R_2}{R_1+R_2}((-V_1)-V_2)≧0・・(7)$$の時出力が反転してV2が低下していきます。この時のV2は最大値となります。式(7)から$$-R_1V_1+R_2V_2 = 0・・(8)$$となり式(6)より$$V_2=-(\frac{R_1}{R_2})V_1+\frac{T}{2CR_3}V_1・・(9)$$となるため式(8)と(9)の関係を整理していくと$$T=4CR_3(\frac{R_1}{R_2})$$となり周期Tが求められます。発振周波数fはTの逆数で求められるので$$f=\frac{1}{4CR_3}(\frac{R_2}{R_1})・・(10)$$となります。
式(10)から周波数が50Hz、三角波の振幅(ピーク電圧)が5Vになるように設計してみます。三角波のピーク電圧はヒステリシス特性で決まるためR1とR2の比率で決まります。R1=10kΩ、R2=20kΩとしたとき式(A)(B)(コンパレータの動作原理)においてVREF=0V、VH=10Vと考えた時VH=5V、VL=-5Vになります。
次に式(1)(式(10)と同じ)からR3を求めます。Cでもよいですが抵抗のほうが調整しやすいためC=0.1uに固定してR3を求めるとR3=100kΩとなります。
PR:企業で求められる即戦力技術を身に付ける テックキャンプエンジニア転職
シミュレーション
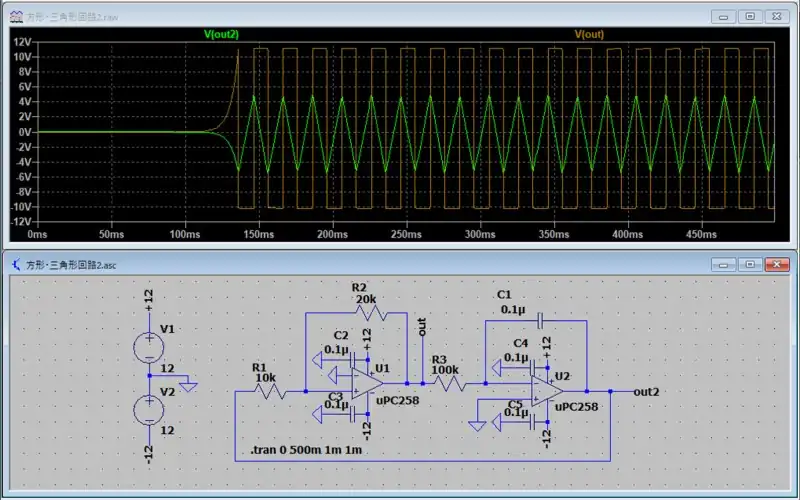
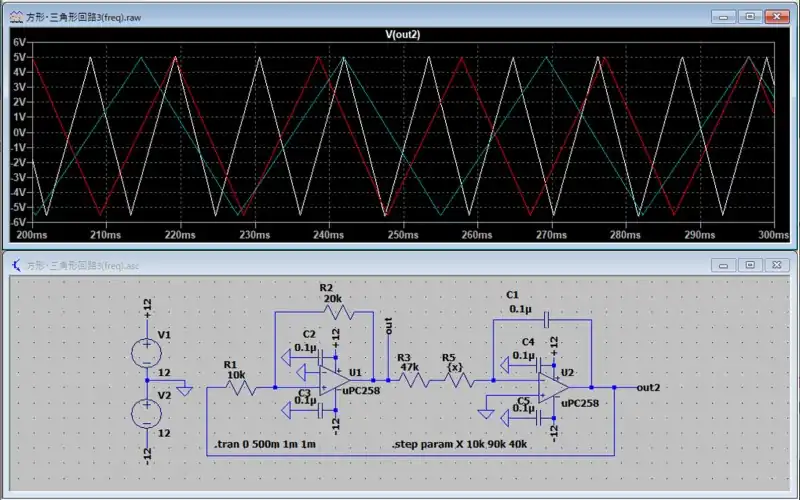
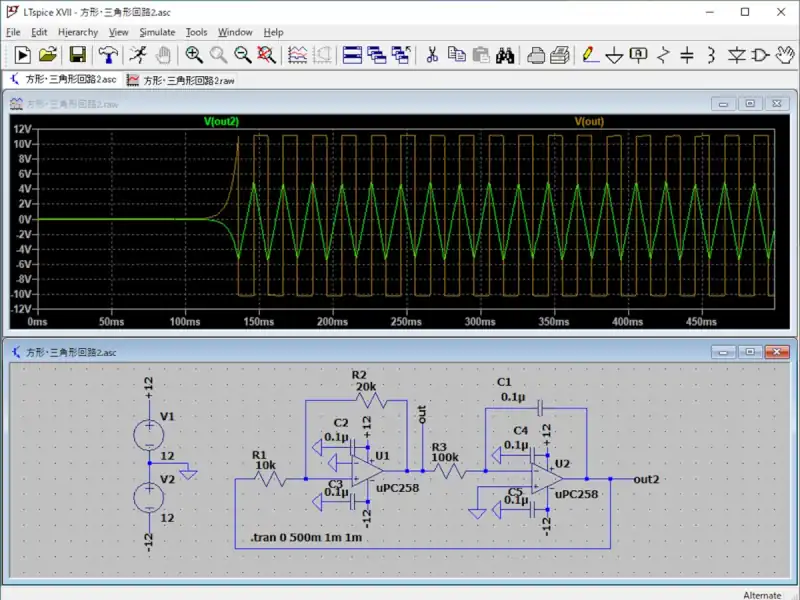
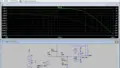
シミュレーションの最初の100msは積分回路のCRの時定数によるものです。方形波と三角波の結果を見ると三角波のピーク値は±5Vになっています。周波数も50Hzになっていることが分かります。
方形波は電源電圧に張り付くように出力されますが、三角波の立上りと立下りに連動して出力していることが分かります。
シミュレーション(デューティ比を変更する)
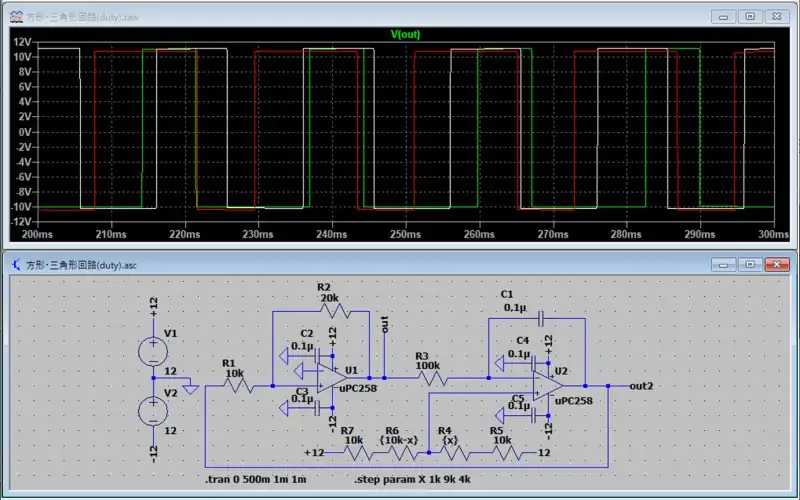
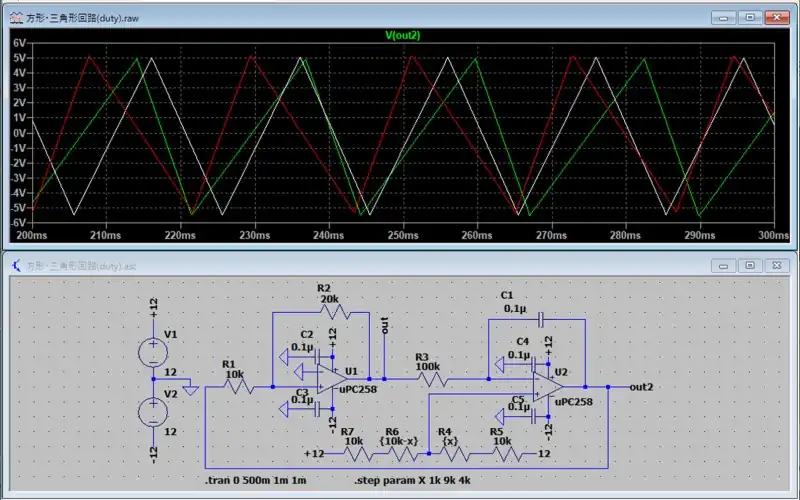
デューティ比(波形のHIGHとLOWの比率)を変更するには積分回路の+ピンの電圧が変更できるように可変抵抗を追加します。
可変抵抗が中央の時(10kΩの可変抵抗なら5kΩが中央)の時にデューティ比が1:1(50%)になります。シミュレーションでは可変抵抗の値がR4を基準としたとき1kΩ,5kΩ,9kΩに変化するように設定しています。
結果を見ると白線がデューティ比が1:1なのでそれを基準にして見てみるとデューティ比が可変できていることが分かります。
PR:わからないを放置せず、あなたにあったスキルを身に着けるコツを教える テックジム 「書けるが先で、理解が後」を体験しよう!
シミュレーション(周波数を変更する)
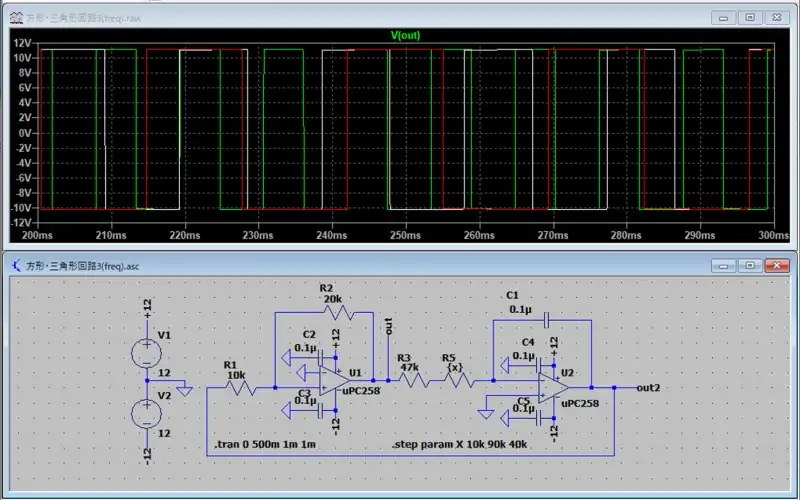
周波数を変更するには積分回路の入力部のR3の抵抗値を変更することで実現できます。R3を固定値として置きR5の可変抵抗が中央値(100kΩの可変抵抗で中央値は50kΩ)の時に50Hz相当になるようにしています。
シミュレーションの青線が50Hz相当になっておりこれを基準にしてみると周波数が変更されていることが分かります。
デューティ比を変更する回路と周波数を変更する回路の双方を実装してデューティ比の変更でずれた周波数を補正して使用することが可能です。
PR:スキマ時間で自己啓発!スマホで学べる人気のオンライン資格講座【スタディング】まずは気になる講座を無料で体験しよう!
積分回路と微分回路
積分回路と微分回路はコンデンサと抵抗によって実現できますが、オペアンプを使って周波数特性を急峻にすることができます。それぞれの特徴と用途について見てみます。
積分回路
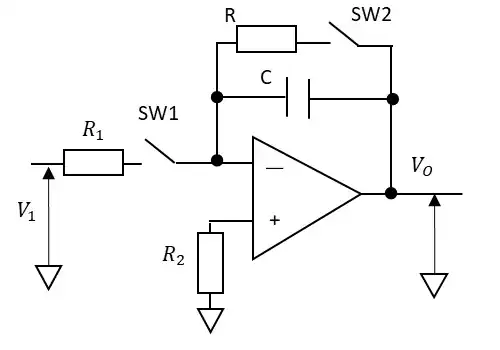
積分回路の特徴:
- 入力電圧V1を時間tについて積分する
- ゼロからの積分の時は放電回路が必要
用途:電圧ー時間変換、波形変換(方形波→三角波)、アナログ演算(積分)
入力バイアス電流とコンデンサの漏れ電流が誤差の原因になるので注意が必要です。
Cはホールド用のコンデンサですが、コンデンサのホールド特性や誘電吸収特性などからセラミック系や電解系は不向きです。セラミックコンデンサは、SW2を短絡解放した後に誘電吸収のため若干電圧が端子間に発生することがあります。この誤差が気になる場合は使用しない方が良いと言えます。
積分回路に使用されるコンデンサはセラミックコンデンサや電解コンデンサよりも漏れ電流や誘電吸収の小さなフィルムコンデンサを使用するとよいでしょう。
積分回路は入力を時間で積分した結果を出力します。時間要素で出力が決まるのでタイマや時間幅を生成する回路(周波数やデューティ比を変更)に使用されます。Cが負帰還されるので正弦波に対しては周波数でゲインが変化するためフィルタとしても利用できます。
動作原理
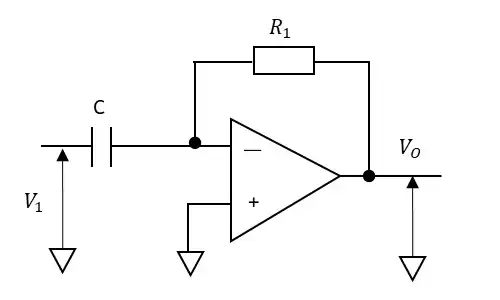
積分回路の原理は主にコンデンサの充放電によるものです。コンデンサCを電流Iで充電するとIの積分が電荷Qになり電圧はVに比例します。Q=CVの関係から$$V=\frac{Q}{C}=\frac{\int{Idt}}{C}$$となります。オペアンプの負帰還から充電電圧は\(I=\frac{V_1}{R}\)であるため$$V_O=-\frac{\int{V_1dt}}{CR}$$となります。CRは時定数です。
実際に使用するときはコンデンサの初期電荷を放電する回路をつける必要があります。以下の手順での動きにより積分値が得られるようになります。
- SW1を開放する
- SW2をONしてコンデンサCの電荷を放電する
- SW2をOFFしてSW1をONして積分を開始する
SW1とSW2の両方をOFFした場合は積分結果の保持となります。上の1~3を繰り返しながら使用します。
PR:(即戦力のスキルを身に着ける:DMM WEBCAMP 学習コース(はじめてのプログラミングコース))
シミュレーション
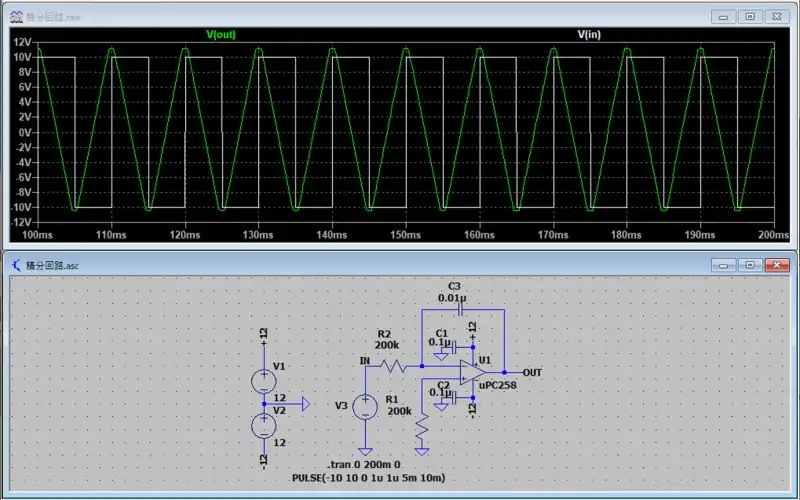
積分回路単体ではオフセットの調整が難しいため後述のコンパレータとセットで使用することが多いです。積分回路の入力にはコンパレータ出力を模擬したデューティ比が1:1(50%)の波形を入力しています。
この結果から一定出力を入力すると出力電圧が傾きを持って上がっていき出力を反転すると下がっていることが分かります。このように積分回路は三角波の生成に使用されます。
微分回路
微分回路は積分回路の抵抗とコンデンサを逆に接続したものですが、ほとんど使用されない回路です。積分回路は一定の入力に対して出力を増加出力できるため利用されることがありますが、微分回路は信号入力のエッジ検出に使用される程度です。微分回路については出力電圧の結果のみ示すと$$V_O=-CR\frac{dV_1}{dt}$$となります。
PR:スキマ時間で自己啓発!スマホで学べる人気のオンライン資格講座【スタディング】まずは気になる講座を無料で体験しよう!
コンパレータ
コンパレータの特徴:
- 入力電圧V1とVREFを比較して結果を2値で出力する。
用途:電圧比較、電圧検出
オペアンプのスルーレートによって応答が制限されることや差動入力範囲が狭いオペアンプの場合は注意が必要です。
コンパレータは入力電圧V1と基準電圧VREFを比較して結果を2値で出力します。2つの電圧を比較したり電圧を閾値と比較して検出するのが主な用途になります。オペアンプに負帰還をかけずに開ループで動作されることでコンパレータとして動作します。
コンパレータは専用のICとして作られており汎用オペアンプよりも使いやすい場合があります。例えばUPC271は出力がオープンコレクタとなっているのでDC5Vでプルアップすることでマイコンへの接続が可能になります。
動作原理
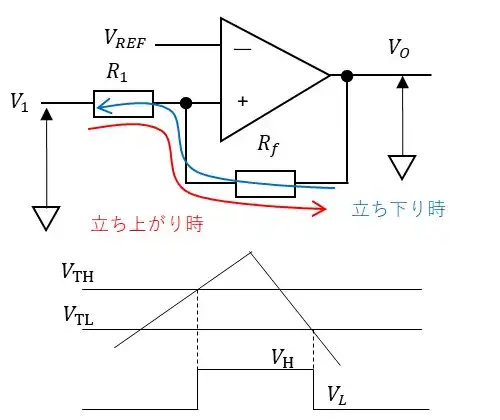
コンパレータは入力のノイズなどで閾値付近で動作を繰り返してしまうことがあるのでヒステリシス特性を持たせることが多いです。ヒステリシス特性の持たせ方について説明します。ヒステリシス特性を持たせたコンパレータをシュミット回路といいます。
入力電圧V1がVTHの時コンパレータが立ち上がったとするとVoはVLOWなので$$\frac{V_{TH}-V_{REF}}{R_1}=\frac{V_{REF}-V_L}{R_f}$$ $$V_{TH}=V_{REF}-\frac{R_1}{R_f}(V_L-V_{REF})=V_{REF}(1+\frac{R_1}{R_f})-\frac{R_1}{R_f}V_L・・(A)$$となります。次に立下り電圧について説明します。入力電圧V1がVTLの時に立ち下がったとすると$$\frac{V_H-V_{REF}}{R_f}=\frac{V_{REF}-V_{TL}}{R_1}$$ $$V_{TL}=V_{REF}-\frac{R_1}{R_f}(V_H-V_{REF})=V_{REF}(1+\frac{R_1}{R_f})-\frac{R_1}{R_f}V_H・・(B)$$となります。
PR:RUNTEQ(ランテック )- マイベスト4年連続1位を獲得した実績を持つWebエンジニア養成プログラミングスクール
シミュレーション
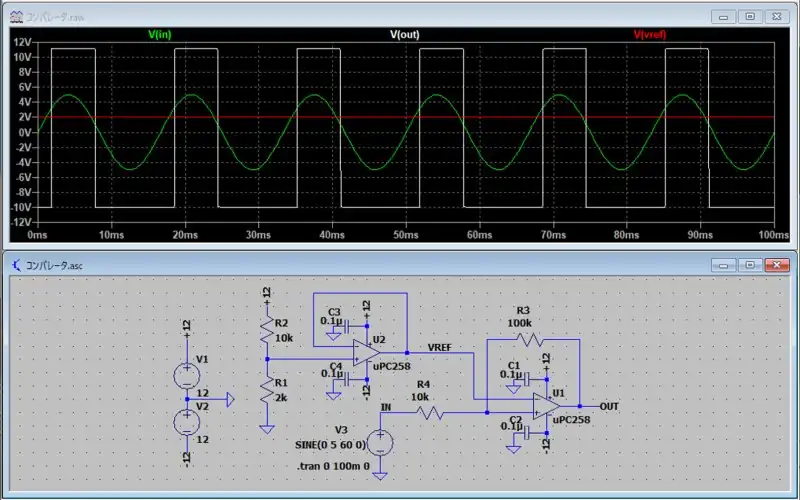
シュミット回路をシミュレーションしました。VREFは分圧した電圧の2Vをボルテージフォロワーを介して基準電圧としています。式(A)と(B)を使用することでVTLとVTHが計算できます。R1(R4)が10kでRf(R3)が100kとして計算するとVTL=1.0V、VTH=3.4Vとなります。
シミュレーションで確認するとVTL=1.0V、VTH=3.4V程でコンパレータの出力が変化していることが分かります。
関連リンク
オペアンプはアナログ入力回路において主役と言っていいほど使用されるため資格試験においてもその特徴を問う問題が出題されます。下記リンクではオペアンプの基本特性と基本回路や私が経験してきたオペアンプの応用回路に関するリンクをまとめています。興味があればご覧ください。
広告
マイベスト4年連続1位を獲得した実績を持つ実践型のプログラミングスクール

最後まで、読んでいただきありがとうございました。

マイコンでポートを制御してSW1とSW2の切り替えを行い任意のタイミングで積分を行うような動きが可能です。スイッチにはTC74HC4066AF(東芝)などを使用するとよさそうです。