【電気電子部門】技術士第一次試験の変圧器の効率に関する問題の解説

こんにちは、ENGかぴです。

技術士第一次試験の電気電子部門の試験において変圧器の効率を求める問題が出題されています。変圧器の鉄損や銅損の意味が分かっていれば解ける問題だと思います。変圧器の負荷に対する効率の求め方や効率が最大になる条件について説明しています。

技術士第一次試験の勉強におすすめする参考書や電気電子部門のポイント解説についてまとめています。これらのシリーズで2か月間勉強することで十分合格できます。

【電気電子部門】技術士第一次試験の勉強におすすめの参考書3選

変圧器の効率に関する問題のポイント解説
1. H30年度の問題
2. R1年度（再試験）の問題
変圧器の考え方
1. 変圧器の損失
2. 変圧器の効率
  1. (1/n)負荷の効率
  2. 変圧器の最大効率
関連するリンク

変圧器の効率に関する問題のポイント解説

変圧器の効率を問う問題が増えていると思います。平成29年度以降で出題が多くなっていると感じます。解き方が分かっていれば簡単に解けるためポイント解説したいと思います。公開されている過去問を引用して説明していきます。

H30年度の問題

この問題のポイントは変圧器における効率の求め方と全負荷時に対するN％負荷時に容量負荷が1/Nになることと銅損$ (\frac{1}{N})^2$乗分が変化することです。

$$効率=\frac{出力}{入力}×100= \frac{出力}{出力+損失}×100=\frac{P}{P+P_i+P_c}×100[％]$$となります。鉄損P_iと銅損P_cとし、出力は容量が1kVAとなっており力率が0.8であるので有効電力からP=1k×0.8=0.8[kW]となります。次に50％負荷時のそれぞれの値を求めます。

負荷が50％(1/2)のとき、有効電力は$ P’=(\frac{1}{2})P= 0.4[kW] $となります。鉄損は電圧の２乗と周波数に反比例するので負荷に関係しません。銅損は変圧器に流れる電流であるので$P_c=I^2×R$の関係から負荷が（1/2）になると$P’_c=(\frac{1}{2})^2P_c$になります。負荷50％時の効率は、

$$負荷50％時の効率=\frac{P’}{P’+Pi+P’_c}×100$$$$=\frac{0.4}{0.4+0.02+(\frac{1}{2})^2 0.06} ×100= \frac{0.4}{0.435}×100=92[％]$$となります。したがって⑤が正解になります。

R1年度（再試験）の問題

この問題のポイントは出力の変化が(900/1000)=(9/10)負荷になっていること変圧器の損失について鉄損が電圧の２乗に比例し、銅損が電流の２乗に比例するという条件が与えられていることです。

出力を1000Wから900Wに変化させた場合について考えると、出力がWで与えられているので負荷の変化のみで考えればよいので$P=(\frac{9}{10})1000 = 900[W] $となります。鉄損は電圧が一定なので変化しません。

銅損が$Pc=(\frac{9}{10})^2 50 = 41[W]$となります。900Wに変化させた場合の効率ηは$$η=\frac{900}{900+ 50 +41}×100= 91[％]$$になります。この段階でアが41で効率が91%となることから④が正解だと分かります。参考として出力電圧が20％低下した場合についても考えます。

出力が一定で電圧が20％低下した状態で鉄損が変化するので変化後の鉄損は$ Pi=(0.8)^2 50 = 32[W]$となります。銅損についても出力が一定で電圧が低下しているので電流が増すことになり、銅損は$ Pc=(\frac{1}{0.8})^2 50 = 78[W]$となります。出力電圧が0.2％低下した場合の効率ηは

$$η= \frac{1000}{1000+ 32 +78}×100= 90[％]$$となります。

以上をまとめると④が正解となります。

変圧器の考え方

変圧器に関して覚えておいたほうが良い公式について説明します。式(1)から(3)までを押さえておけば対応できると思います。

変圧器の損失

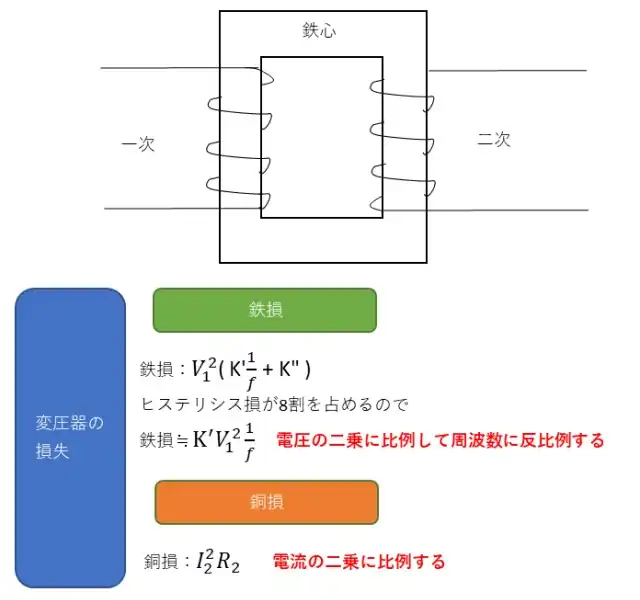
変圧器を構成する主なものは鉄心と巻線となるので鉄心から生じる鉄損と巻線から生じる銅損が変圧器の主な損失となります。鉄損は変圧器を一定電圧で一定周期で使用すると負荷に関係なく不変となり無負荷損とも言われます。

その他には励磁電流による損失もありますが、損失がわずかなため無視しても影響がないことが多いです。

鉄損は多くの実験によりヒステリシス損P_hと渦電流損P_eの和であることが分かっているので鉄損をP_iとすると$$P_i = P_h + P_e = K’\frac{V^2}{f}+K”V^2=V^2(K’\frac{1}{f}+K”)$$となります。

ヒステリシス損は鉄損の８割を占めると言われているので、鉄損は電圧の２乗に比例し電圧を一定にすると周波数に反比例することになります。

銅損は負荷電流が流れたために生じる巻線の抵抗損であって負荷電流の２乗に比例するもので負荷損とも言われます。

２次側に負荷をつないだ時に流れる負荷電流Iによって一次、二次巻線r₁、r₂に生じる損失で銅損をP_cとすると$$P_c=I^2 r_1+I^2 r_2[W]$$となります。

aを一次側と２次側の巻き数の比としたとき一次側に換算した抵抗R₁とすると$R1=r_1 +a^2 r_2$となり２次側に換算したした抵抗をR_2とすると$R_2=\frac{r_1}{a^2}+r_2$となり、$$P_c=I_{1}^{2}R_{1}=I_{2}^{2}R_{2}$$となります。1次側や2次側に換算したとしても電流の負荷電流の2乗に比例します。

巻線に負荷電流が流れると漏れ磁束が増し、この磁束が巻線や鉄の構造物を通ることで漂遊負荷損を生じます。負荷電流が流れて生じる損失は銅損+漂遊負荷損となります。漂遊負荷損は銅損の5~30%発生しますが、100kVA以下の変圧器であれば無視できます。

変圧器の効率

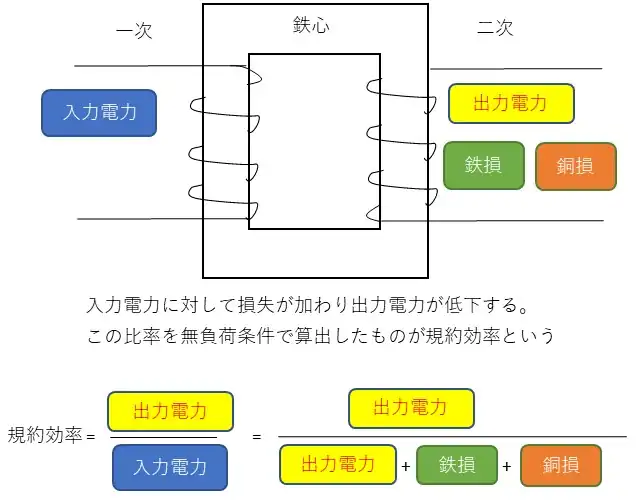
変圧器の効率は発生した出力と入力した電力の比をパーセントで表します。電力の比になるので変圧器の容量であるVAに対して力率から有効電力を求める必要があります。

電圧と電流の掛算すると皮相電力となり定格容量になります。有効電力=皮相電力×力率の関係から入力電力を求めることができます。出力は入力に損失分が加わることから必ず100％未満になります。

$$規約効率η= \frac{出力}{入力}×100=\frac{出力}{出力+損失}×100$$$$=\frac{V_{2}I_{2}cosθ_{2}}{V_{2}I_{2}cosθ_{2}+P_i+P_c}×100[％]・・(1)$$

ここでV₂は二次定格電圧[V]、I₂は二次定格電流[A]、cosθ₂は負荷力率、P_iは鉄損[W]、P_cは銅損[W]です。

PR：恥ずかしさゼロの英会話練習【トーキングマラソン】先生とのレッスンは緊張する、発音が下手だから恥ずかしいという方、今すぐ無料体験！

(1/n)負荷の効率

負荷が(1/n)の時、鉄損P_iは一定ですが、負荷電流I₂が(I₂/n)となり、銅損P_cは$(\frac{I_2}{n})^2×R_2$であるから$(\frac{1}{n})^2$に減少します。この時の効率η₂は

$$η_2=\frac{\frac{1}{n}V_2 I_2 cosθ_2}{\frac{1}{n}V_2 I_2 cosθ_2 + P_i+(\frac{1}{n})^2 P_c}×100[％]・・(2)$$

となります。

変圧器の最大効率

変圧器の効率が最大になる条件について考えます。式(1)から分母分子をI₂で割ると$$η_3=\frac{V_{2}cosθ_{2}}{V_{2}cosθ_{2}+\frac{P_i}{I_2}+I_2R_2}×100[％]$$η₃が最大になるためには分母の$\frac{P_i}{I_2}+I_2R_2 $が最小になればよいことが分かります。

最小の定理「正の2変数の積が一定の場合2変数が相等しければ2変数の和は最小になる」を適用して考えると$\frac{P_i}{I_2}×I_2R_2=P_iR_2 ・・P_iR_2$は一定となるので$\frac{P_i}{I_2}=I_2R_2$の場合に最小になります。$P_i = I_2^2R_2$となるので鉄損=銅損となったとき最大になります。

鉄損と銅損が最大効率になる負荷が(1/n)であるとき$P_i = (\frac{1}{n})^2 P_c$から$$\frac{1}{n}=\sqrt{\frac{P_i}{P_c}}=\sqrt{\frac{鉄損}{銅損}}・・(3)$$のとき最大効率になります。