こんにちは、ENGかぴです。
技術士第一次試験や電気主任技術者の問題を解いていると消費電力が最大になる抵抗値を求めるような問題があります。これらの問題はインピーダンスマッチングの意味が分かっていれば計算しなくても答えが出るものがありますので解き方について記事にしました。インピーダンスマッチングとは
電気主任技術者や技術士第一次試験のように低周波数を扱った場合のインピーダンスマッチングについて説明します。
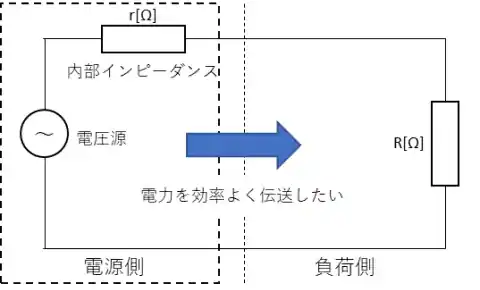
一般的に電源は電圧源と抵抗（インピーダンス）によって構成されています。簡単な回路図で示すとイラストのようになります。
電源には電圧源と内部インピーダンスがあります。
電源装置によっては位相を持っていたりすることからインピーダンスと表現していますが、簡単のために抵抗分だけで考えます。
一般的に電源側の内部インピーダンスは小さいので負荷側のRが大きければ電流はRの依存します。Rが小さくなるとより多くの電流が流れることになるのでｒが小さくても電圧降下が発生してしまいます。
インピーダンスマッチングとは簡単に言うと電源側から負荷側に最大の効率で電力を伝送することです。最大の効率とは消費電力が最大になることと同じです。
電源をEとしてRの消費電力を求めると
$$P=E^2\frac{R}{(R+r)^2}=E^2\frac{1}{(R+2r+\frac{r^2}{R})}・・（A)$$
になります。この時のPの最大値を求めようとすると（A)式において分母が最小となる（傾きが0）ときになるので分母を微分して解く必要があります。
分母をRで微分\(= 1 – \frac{r^2}{R^2} = 0\)となるのでR>0よりR=rになります。つまり、R=rのときに消費電力が最大になるということです。
これをEが5V、ｒが10オームであるときにRの値を0.1Ω毎にプロットした時の消費電流をシミュレーションしてみると以下のようになります。
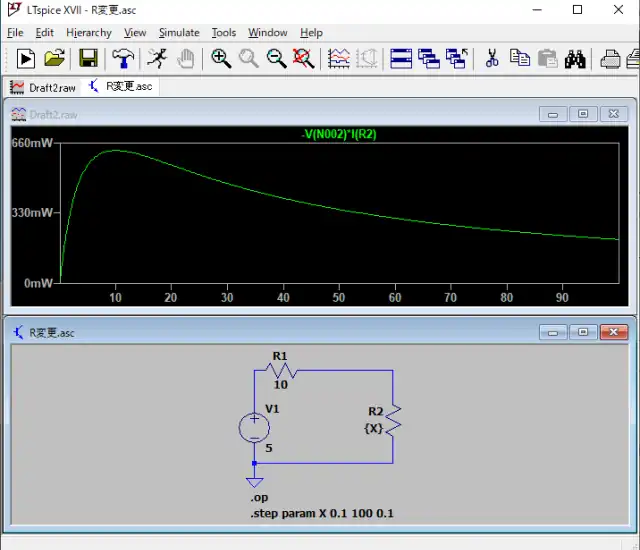
R=10の時が最大になります。シミュレーションでもその結果が見て取れます。消費電力が最大となるように入力側と出力側のインピーダンスを調整することをインピーダンスマッチング（インピーダンス整合）といいます。
厳密にインピーダンスマッチングを考える必要があるのは高周波を取り扱う場合で音声信号や商用電源を扱いような周波数帯域においてはそれほど重要ではありません。
これらを考えるときは長距離伝送回路について学習する必要がありますが、上記資格試験においては商用電源を対象にしていることが多いこともありインピーダンスマッチングの意味を知っておけば対応はできます。
問題の意図からインピーダンスマッチングを考える
技術士第一次電気電子分野と電気主任技術者3種の過去問を使ってインピーダンスマッチングの考え方から問題を楽に解く方法について考えてみたいと思います。
技術士第一次試験電気電子の問題
実際に技術士第一次試験電気電子分野で出題された問題について見てみます。
H27年度の問題
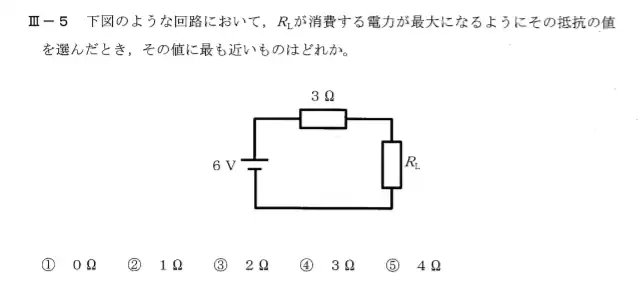
これを普通に解いてみます。回路に流れる電流I[A]は次のようになります。$$I= \frac{6}{3+R_L}$$この時RLが消費電力Pは以下の通りとなります。$$ P=R_L×I^2=\frac{36}{(R_L+6+\frac{9}{R_L})}$$上記式において分母が最小になるときが消費電力が最大となるので分母をRLで微分すると$$分母をR_Lで微分=1-\frac{9}{R_L^2}=0$$ $$R_L^2= 9(R_L>0)$$ $$R_L=3[Ω]$$したがって3Ωとなるので④が正解となります。
このように解いた場合は、微分が分からなかった場合は詰んでしまいます。ここで問題ももう一度見てみると「RLが消費する電力が最大となるように」とあります。
インピーダンスマッチングが消費電流を最大にすることであると分かっていれば問題の図を見ただけで計算することなく答えが分かります。
この問題の場合は、題意からインピーダンスマッチングの抵抗が問われていることが分かるのでRLから電源側を見た抵抗がそのまま答えになるので一瞬で④が正解だと分かります。
H28年度の問題
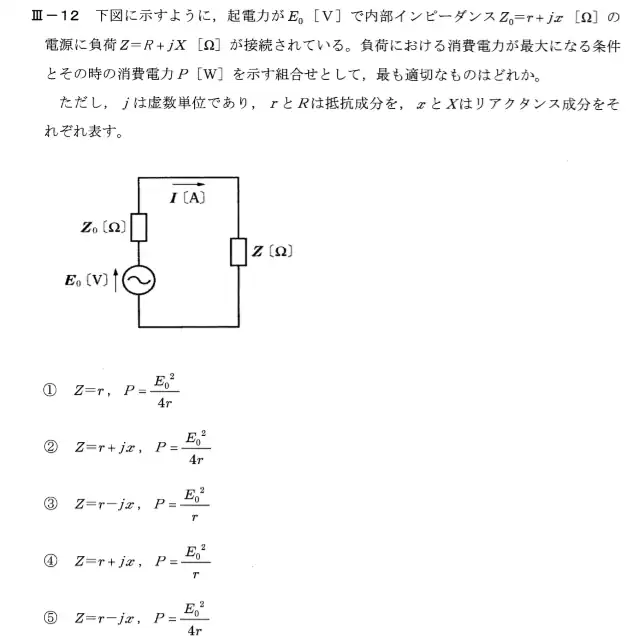
これを普通に解いてみます。回路全体のインピーダンスはZ+Z0=r+R+j(x+X)になります。
消費電力が最大ということは虚数部が0になるのでX=-xとなります。このことから抵抗分のみで考えることになります。
消費電力Pは以下の通りとなります。$$ P=\frac{E0^2}{(\frac{r^2}{R}+R+2r)}$$上記式において分母が最小になるときが消費電力が最大となるので分母をRで微分すると$$分母をRで微分=-\frac{r^2}{R^2}+1=0$$ $$R^2= r^2(R>0)$$ $$R=r$$したがってZ=r-jxとなります。消費電流Pは$$P=\frac{rE0^2}{(2r)^2}=\frac{E0^2}{4r}$$となるので⑤が正解となります。
インピーダンスマッチングの考え方を使って解いてみます。
この問題では、「内部インピーダンスがとあることと負荷の消費電力が最大になるとき」とあります。インピーダンスマッチングの考え方によって答えがすぐにわかります。この問題のポイントは虚数部があったとしても消費電力を求めるので虚数部が0になるということです。
このことが分かっていれば答えが③と⑤に絞り込むことができます。インピーダンスマッチングの考えによって抵抗分もR=rになることが分かるので負荷Zにかかる電圧は2つのrで分圧することになるので負荷Zの電圧Vは\(\frac{E0}{2} \)になります。消費電力Pは$$P=\frac{V^2}{r}=\frac{E0^2}{4r}$$となり⑤が答えになります。
電気主任技術者3種の問題
実際に、電気主任技術者3種で出題された問題を見てみます。数年ごとに似たような問題が出ています。
例）2007年理論の問題
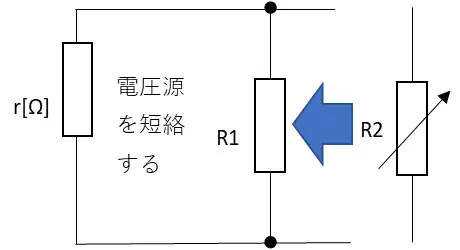
起電力がE[V]で内部抵抗がr[Ω]の電池がある。この電池に抵抗R1[Ω]と可変抵抗R2[Ω]を並列につないだとき、抵抗R2[Ω]から発生するジュール熱が最大となるときの抵抗R2[Ω]の値を表す式として正しいのはどれか。
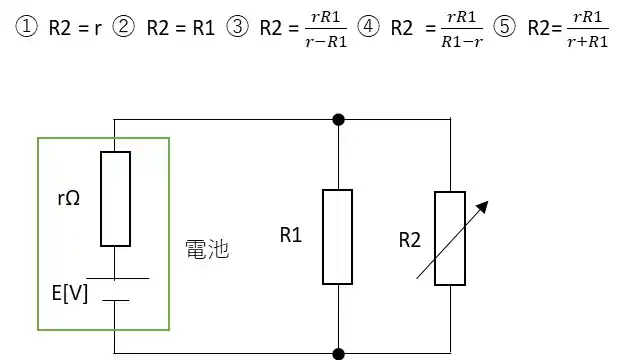
上の図は、問題にはありません。問題を読んで問題を解く際に自分で考える必要があります。この問いには、抵抗R2[Ω]から発生するジュール熱が最大とあります。これは言い換えると消費電力が最大になっているということです。つまりインピーダンスマッチングの考え方が使えます。
R2からみたインピーダンスとR2が一致するときに消費電力が最大になるになるということになります。
R2から見たインピーダンスは電圧源を短絡したときの合成抵抗になります。
rとR1の合成抵抗がR2になるので$$R2=\frac{rR1}{r+R1}$$の時にジュール熱が最大となるので答えは⑤になります。
最後まで、読んでいただきありがとうございました。
3Ωが電源側の内部インピーダンスダンスだと考えると電源側と負荷側においてインピーダンスマッチングをするために何Ωの抵抗が必要ですかという問題になります。